Hans Walser, [20201209]

Falsches Dodekaeder

Anregung: Walter Arn, Flawil

1 Worum geht es?

Approximationsmodelle für das reguläre Dodekaeder

2 Standardbeispiel

Die Abbildung 1 zeigt ein Kantenmodell eines regulären Dodekaeders.

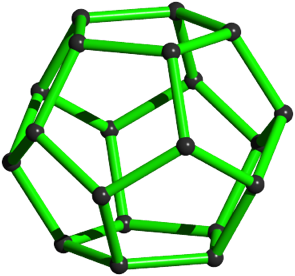
Abb. 1: Dodekaeder

Die Abbildung 2 zeigt ein Modell, das wie ein Dodekaeder aussieht.

Abb. 21: Dodekaeder?

Das Modell der Abbildung 2 ist aus einem Baukasten für Chemie-Studierende gebaut.

Die Knotenelemente (Abb. 3a) haben eine Tetraedersymmetrie mit vier Andockbolzen, um welche Röhrchen als Verbindungsstücke aufgesteckt werden können (Abb. 3b).

Abb. 3: Eckverbindungen

Die Endpunkte der vier gleich langen Röhrchen bilden ein reguläres Tetraeder. Das heißt aber, dass zwei Röhrchen paarweise einen Winkel von einschließen. Dies ist der berühmte kristallografische Winkel. Er ist auch der stumpfe Schnittwinkel zweier Raumdiagonalen im Würfel. Weiter ist er der Diederwinkel (Flächenwinkel) im regulären Oktaeder. Er kommt also bei den drei platonischen Körpern Tetraeder, Würfel und Oktaeder vor, nicht aber beim regulären Dodekaeder oder Ikosaeder. Daher zeigt die Abbildung 2 eine „Fälschung“.

Die Seitenflächen des regulären Dodekaeders sind reguläre Fünfecke. Diese haben Innenwinkel von 108°. Der Fehler beträgt also etwa anderthalb Grad. Dieser Fehler wird durch die Elastizität des Materials aufgefangen. Von Auge ist er nicht wahrnehmbar.

Alle folgenden Modelle weisen im Prinzip denselben Fehler auf.

Bemerkung: der kristallografische Winkel ist auch der stumpfe Schnittwinkel der Diagonalen in einem Rechteck im DIN-Format, also zum Beispiel bei einem DIN A4 Papier (Abb. 4, Walser 2013).

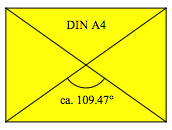
Abb. 4: Kristallografischer Winkel

3 Abgestumpfte Tetraeder

Die Abbildung 5 zeigt eine Dodekaeder-Approximation aus abgestumpften Tetraedern. Das Modell wurde von Rahel Baumann, Flawil, gebaut. Jede Ecke des Dodekaeders besteht aus einem abgestumpften Tetraeder.

Abb. 5: Dodekaeder-Approximation (Foto Walter Arn)

Die Abbildungen 6 und 7 zeigen die Herstellung eines abgestumpften Tetraeders. An den Ecken des Tetraeders werden kleine Tetraeder abgeschnitten, deren Kantenlänge ein Drittel der Kantenlänge des Starttetraeders beträgt.

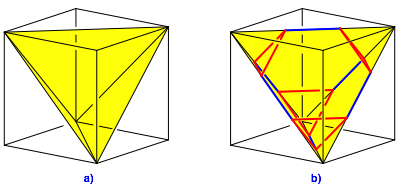
Abb. 6: Tetraeder im Würfel

Durch das Abschneiden entsteht ein Körper, dessen Oberfläche aus vier regulären Dreiecken und aus vier regulären Sechsecken besteht.

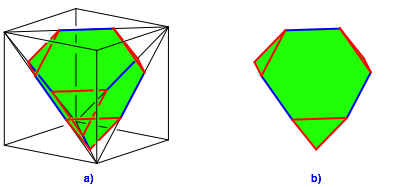
Abb. 7: Abgestumpftes Tetraeder

Im Modell der Abbildung 5 sind die abgestumpften Tetraeder an den Dreiecksflächen verklebt worden. Die (ausgedehnten) Ebenen dieser Dreiecke schneiden sich unter dem kristallografischen Winkel.

Für den Bau eines abgestumpften Tetraeders braucht es zunächst vier gleichseitige Dreiecke aus Papier (Abb. 8a). Die äußeren Drittel-Ecken werden dann nach hinten gebogen. Je drei kleine Dreiecke von drei Bauteilen werden verklebt. An den blauen Sechseckkanten hat das Modell des abgestumpften Tetraeders einen Schlitz. Dies ist in der Abbildung 5 gut sichtbar.

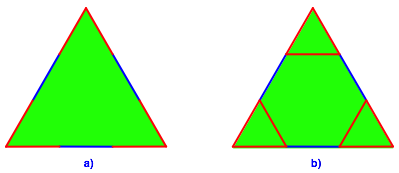
Abb. 8: Bauteil

4 Abgestumpfte Würfel

Die Abbildung 9 zeigt eine Dodekaeder-Approximation aus abgestumpften Würfeln.

Abb. 9: Dodekaeder-Approximation

Die Abbildung 10 zeigt die Konstruktion der abgestumpften Würfel. Der Würfel wird an drei Ecken abgestumpft, welche je zwei Kantenlängen voneinander entfernt sind. Die Ecken wurden bis zur Kantenmitte abgestumpft. Man hätte aber auch mehr oder weniger abstumpfen können. In der Abbildung 10a sehen wir drei von der Mitte ausgehende Halbdiagonalen, welche den kristallografischen Winkel einschließen.

Zwei benachbarte Bauteile werden an den Dreiecksflächen verklebt.

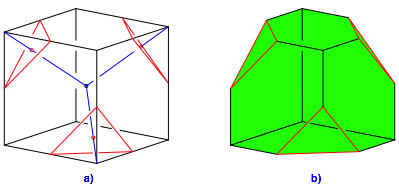
Abb. 10: Abgestumpfter Würfel

Statt Ecken abstumpfen, können wir auch Ecken eindrücken (Abb. 11).

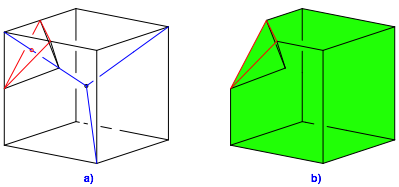
Abb. 11: Eingedrückte Ecke

Allerdings müssen dann an den einzelnen Würfelchen unterschiedlich viele Ecken eingedrückt werden. Die Symmetrie ist ein bisschen im Eimer.

Die Abbildung 12 zeigt ein Dreistreifen-Flechtmodell eines Würfels mit einer eingedrückten Ecke.

Abb. 12: Eingedrückte Ecke

Die Abbildung 13 zeigt das Schnitt- und Faltmuster der drei Streifen.

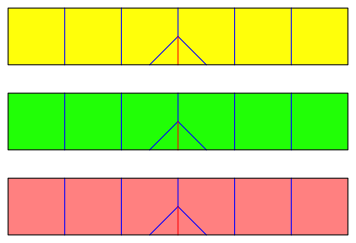
Abb. 13: Schnitt- und Faltmuster

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.

Website

Hans Walser: Würfel mit eingedrückten Ecken

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfel_eing_Ecken/Wuerfel_eing_Ecken.pdf