Hans Walser, [20100523a]

Falten im Rechteck

Anregungen: E.-R. M., S. und H. S., S.

1        Ecke hinauffalten

In einem Hochformat-Rechteck falten wir die rechte untere Ecke auf die obere Kante. Dann falten wir wieder zurźck.

 

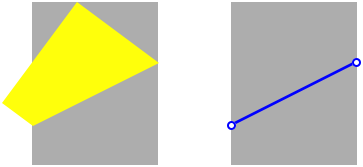
Faltlinie

 

Wir fragen nun, wie die Faltlinie die senkrechten Rechtecksseiten teilt.

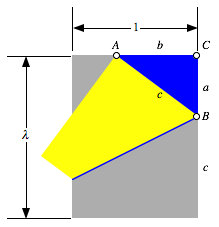
2        Ma§e und Bezeichnungen

Das Rechteck habe die Breite 1 und die Hšhe . Bezeichnungen gemŠ§ Figur.

 

Bezeichnungen

 

Fźr die folgenden †berlegungen verwenden wir b als freien Parameter.

3        Teilpunkt am rechten Rand

In welchem VerhŠltnis teilt der Punkt B die rechte Rechtecksseite?

Es ist zunŠchst . Aus dem blauen rechtwinkligen Dreieck ABC ergibt sich:

 

 

 

 

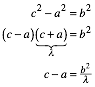
Aus  und  erhalten wir:

 

 

 

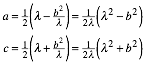
Daraus ergibt sich:

 

 

3.1      Rationales TeilverhŠltnis

Satz 1

 

Falls , dann

 

Beispiel:  (DIN-Format). Mit  erhalten wir am rechten Rand ein rationales TeilverhŠltnis.

3.2      Pythagoreisches Dreieck

Falls , dann ist auch .

Mit ,  und ,  erhalten wir fźr das blaue rechtwinklige Dreieck ABC:

 

 

 

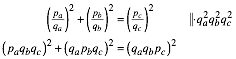
Das Dreieck ABC ist also ein pythagoreisches Dreieck.

Satz 2

 

Mit  ergibt sich ein pythagoreisches Dreieck ABC.

 

Beispiele:

1.     Origami-Papier. Es ist . Mit  erhalten wir ein pythagoreisches Dreieck.

2.     US-Letter-Format. Es ist . Mit  erhalten wir ebenfalls ein pythagoreisches Dreieck.

4        Teilpunkt am linken Rand

Wir ergŠnzen die Bezeichnungen:

 

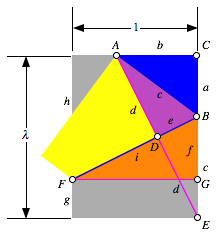
Bezeichnungen

 

In welchem VerhŠltnis teilt der Punkt F die linke Rechtecksseite?

ZunŠchst ist . Daraus ergibt sich:

 

 

 

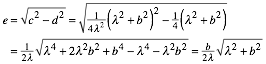
Da die Dreiecke BAD (magenta) und BFG (orange) Šhnlich sind, folgt:

 

 

 

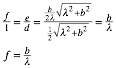
Fźr g erhalten wir:

 

 

Fźr h ergibt sich:

 

 

Es ist also:

 

 

 

 

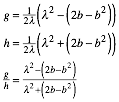
Satz 3

 

Fźr  und  ergibt sich am linken Rand ein rationales TeilverhŠltnis.

 

Beispiel: DIN-Format und .

5        LŠnge der Faltstrecke

Fźr die LŠnge i erhalten wir:

 

 

Wegen der Wurzel ist i in der Regel nicht rational.

6        Beispiele

6.1      Origami

Wir arbeiten mit quadratischem Papier, also .

6.1.1    b = 0.5

Fźr  ergibt sich:

 

 

 

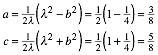
Wir erhalten mit  das einfachste pythagoreische Dreieck.

 

    

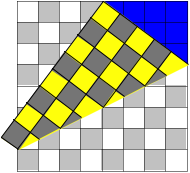
Pythagoreisches Dreieck

 

Am linken Bildrand haben wir das TeilverhŠltnis . Die Figur passt in ein Schachbrett. 

6.1.2    b = 0.75

Fźr  ergibt sich:

 

 

 

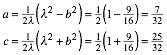
Wir erhalten das pythagoreische Dreieck mit . Weiter ist:

 

 

 

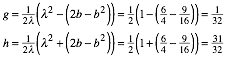
Und schlie§lich gilt in diesem Beispiel:

 

 

Es sind also alle beteiligten Strecken (inklusive i) in einem rationalen VerhŠltnis.

 

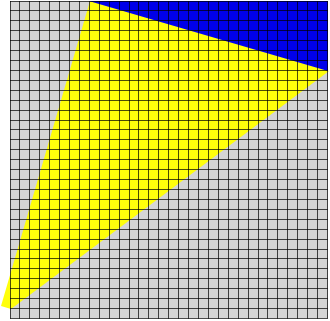
Situation im Raster

6.1.3    Allgemein

Allgemein ergibt sich fźr :

 

 

 

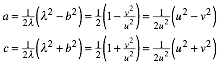
Somit ist:

 

 

Das sind die źblichen Formeln zur Generierung der pythagoreischen Zahlentripel.

6.2      Das DIN-Format

Nun ist . Wir erhalten die Formeln:

 

 

 

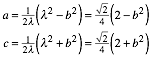
Ebenso:

 

 

 

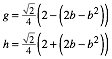
Und:

 

 

6.2.1    b = 1

Fźr  ergibt sich . Dieses Beispiel verdanke ich H. S. .

 

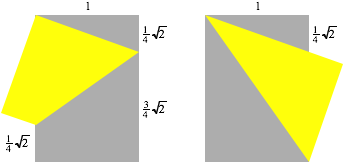
b = 1

 

Statt zwei diametrale Ecken aufeinander zu falten, kšnnen wir auch lŠngs der zugehšrigen Diagonalen falten.

6.2.2    b = 0.5

Das Beispiel findet sich in

http://www.wissenschaftsreisen.de/quiz.php?rechts=quiz/quiz-2008-7.html

und

http://www.wissenschaftsreisen.de/quiz.php (Lšsung des PreisrŠtsels vom Juli 2008)

In diesem Beispiel erhalten wir aus :

 

 

Es sind also — mit Ausnahme von b — alle Zahlen in einem rationalen VerhŠltnis zu einander. Die Figur passt in ein DIN-Raster.

 

DIN-Raster

 

6.2.3    b = 7/6

Das Beispiel ist etwas subtil, indem wir fźr  die Oberkante des Rechteckes nach links verlŠngern mźssen. Wir erhalten:

 

 

Mit Ausnahme von b stehen alle Zahlen in einem rationalen VerhŠltnis zueinander.

 

Die verlŠngerte Oberkante

 

6.2.4    Kombination mit gleichseitigem Dreieck

Wir wŠhlen nun . Damit ergibt sich:

 

 

Wir haben am rechten Rand ein rationales TeilverhŠltnis, am linken Rand nicht.

 

Kombination mit gleichseitigem Dreieck

 

6.3      Goldenes Rechteck

Nun sei . Wir erhalten:

 

 

Wir haben keine rationalen VerhŠltnisse auf der linken und der rechten Rechtecksseite.

 

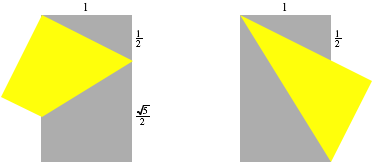
Goldenes Rechteck

 

Statt zwei diametrale Ecken aufeinander zu falten, kšnnen wir auch lŠngs der Diagonalen falten.

6.4      Wurzel-3-Rechteck

Wir arbeiten mit  und . Das ergibt:

 

 

Mit Ausnahme von b stehen alle Zahlen (inklusive i) in einem rationalen VerhŠltnis zueinander.

 

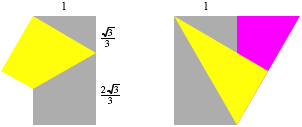
Gleichseitiges Dreieck

 

Statt zwei diametrale Ecken aufeinander zu falten, kšnnen wir auch lŠngs der Diagonalen falten. Dann kšnnen wir zum gleichseitigen Dreieck ergŠnzen. Das TeilverhŠltnis am rechten Rand entspricht dem TeilverhŠltnis der Schwerlinien.