1 Worum geht es?

Spiel mit rgb-Farben auf der Kugeloberfläche

2 Farbrechteck

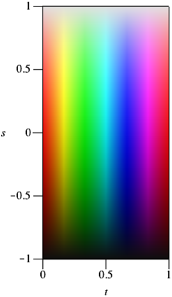
Abb. 1: Farbrechteck

Das Farbrechteck (Abb. 1) zeigt in der horizontalen Richtung (Parameter t = 0..1) die Farben des Farbkreises. In vertikaler Richtung (Parameter s = –1..1) variieren die Farben von schwarz bis weiß.

Dieses Farbrechteck wird generiert wie folgt.

Wir definieren drei Funktionen der Variablen t:

roth := t -> min(max(2-abs(abs(6*(t-0/3) - 3) - 3), 0), 1):

grun := t -> min(max(2-abs(abs(6*(t-1/3) - 3) - 3), 0), 1):

blau := t -> min(max(2-abs(abs(6*(t-2/3) - 3) - 3), 0), 1):

Diese drei Funktionen ergeben im rgb-System für t = 0..1 den Farbkreis.

Weiter definieren wir eine Funktion in (x,y):

f := (x,y) -> (0.5 - y)*x^2 + 0.5*x + y:

Es ist f(–1, y) = 0 (schwarz), f(0, y) = y (y), f(1, y) = 1 (weiß)

Damit bauen wir drei weitere Funktionen:

roth2 := (s,t) -> f(s, roth(t)):

grun2 := (s,t) -> f(s, grun(t)):

blau2 := (s,t) -> f(s, blau(t)):

Diese drei Funktionen verwenden wir im rgb-System für das Farbrechteck der Abbildung 1.

3 Modifiziertes Farbrechteck

Abb. 2: Parameterrechteck für Kugel

Wir modifizieren das Farbrechteck so dass es als Parameterrechteck für die übliche Kugelparametrisierung passt (Abb. 2).

Die Abbildung 3 zeigt die zugehörige Farbkugel.

4 Farbkugel

4.1 Ansicht

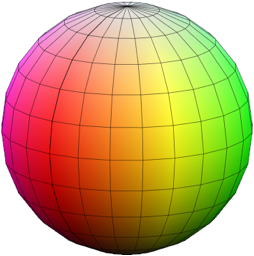
Abb. 3: Ansicht

4.2 Spezielle Sichten

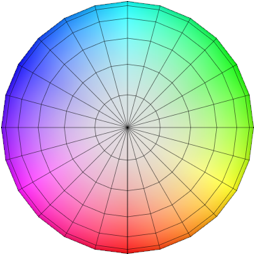
Abb. 4.1: Sicht von oben

Im Zentrum (Nordpol) sollte es weiß sein. Das ist offenbar nicht so gut geraten.

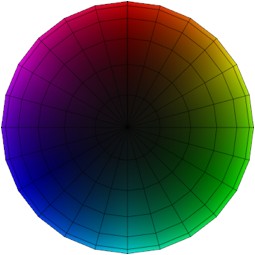
Abb. 4.2: Sicht von unten

Abb. 4.3: Sicht von vorne

Abb. 4.4: Sicht von rechts

Abb. 4.5: Sicht von hinten

Abb. 4.6: Sicht von links

Websites

Hans Walser: Farbkreis

http://www.walser-h-m.ch/hans/Miniaturen/F/Farbkreis/Farbkreis.htm

Hans Walser: Farbwürfel

http://www.walser-h-m.ch/hans/Miniaturen/F/Farbwuerfel2/Farbwuerfel2.htm

Hans Walser: Farbwürfel

http://www.walser-h-m.ch/hans/Miniaturen/F/Farbwuerfel/Farbwuerfel.htm