1 Worum geht es?

Zerlegung von Quadern. Raumvorstellung. Teilbarkeit. Paritätsproblem.

2 Fast-Würfel

Unter einem Fast-Würfel verstehen wir einen Quader mit drei aufeinanderfolgenden natürlichen Zahlen als Kantenlängen.

Die Abbildung 1 zeigt das Beispiel mit den Kantenlängen 7, 8 und 9.

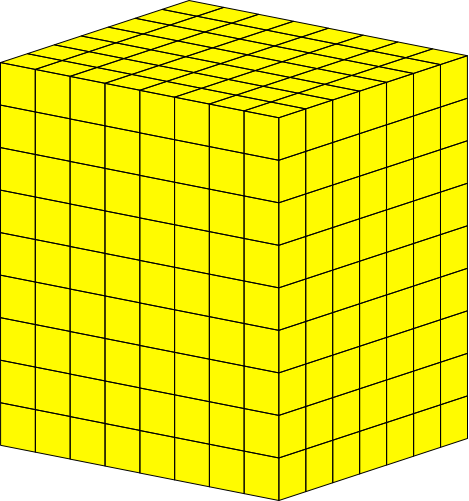
Abb. 1: Kantenlängen 7, 8 und 9

3 Konstruktion aus dem Würfel

Wir beginnen mit einem Würfel der Kantenlänge n und nehmen eine Kante weg (Abb. 2 für n = 5). Die Restfigur hat somit das Volumen n³ – n.

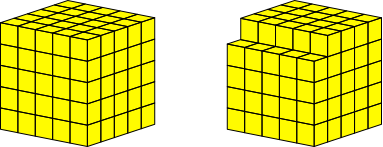
Abb. 2: Wegnahme einer Kante

Nun schneiden wir vorne die Platte der Dicke 1 ab und setzen sie oben an (Abb. 3). Der entstehende Quader hat die Kantenlängen n – 1, n und n + 1, ist also ein Fast-Würfel.

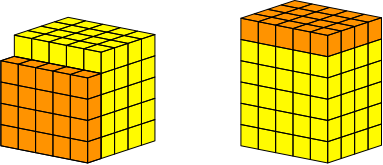
Abb. 3: Versetzen einer Platte

Der Fast-Würfel mit den Kantenlängen n – 1, n und n + 1 hat somit das Volumen n³ – n. Dies kann natürlich auch direkt berechnet werden:

(n – 1) n (n + 1) = n (n – 1) (n + 1) = n (n² – 1) = n³ – n

Bei drei aufeinanderfolgenden natürlichen Zahlen sind eine oder zwei Zahlen gerade, also durch 2 teilbar, und genau eine durch 3 teilbar. Somit ist n³ – n in jedem Fall durch 6 teilbar.

4 Zerlegung in sechs kongruente Quader

Die Frage ist nun, ob sich ein Fast-Würfel auch in sechs kongruente Quader mit ganzzahligen Kantenlängen zerlegen lässt, und wenn ja, auf wie viele Arten dies geht.

Die Abbildungen 4 zeigen zunächst die Fast-Würfel für n = 2 .. 9. Es sind jeweils drei Exemplare angegeben. Die geneigte Leserin oder der geneigte Leser ist eingeladen, durch Ausmalen auszuprobieren, ob und wie oft es geht.

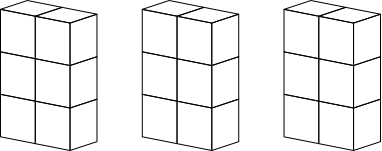
Abb. 4.2: 1×2×3

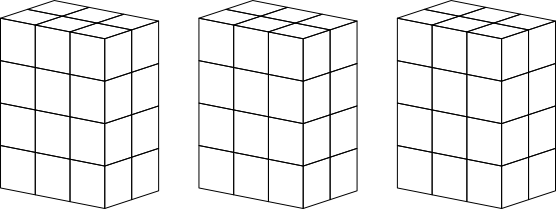
Abb. 4.3: 2×3×4

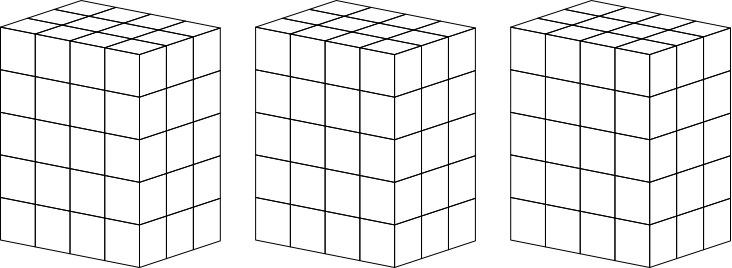
Abb. 4.4: 3×4×5

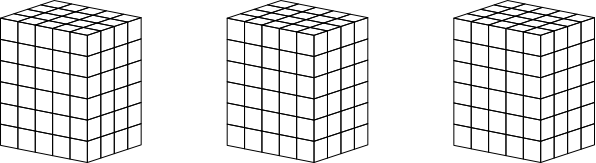
Abb. 4.5: 4×5×6

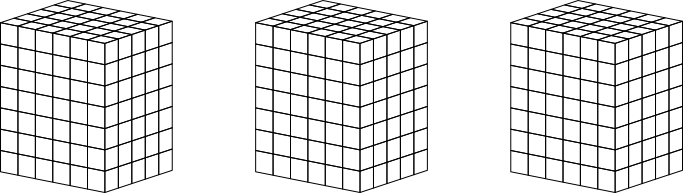
Abb. 4.6: 5×6×7

Abb. 4.7: 6×7×8

Abb. 4.8: 7×8×9

Abb. 4.9: 8×9×10

5 Ein Paritätsproblem

Die Abbildungen zeigen die Lösungen. Es gibt im Wechsel eine oder zwei Lösungen.

Abb. 5.2: 1×2×3

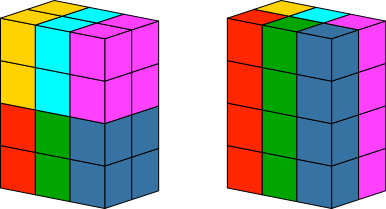
Abb. 5.3: 2×3×4

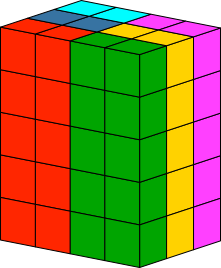
Abb. 5.4: 3×4×5

Abb. 5.5: 4×5×6

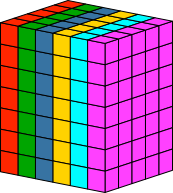
Abb. 5.6: 5×6×7

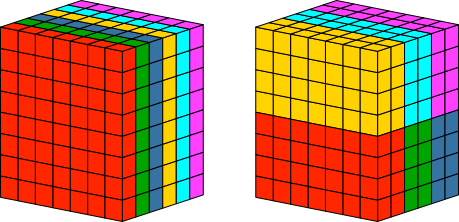
Abb. 5.7: 6×7×8

Abb. 5.8: 7×8×9

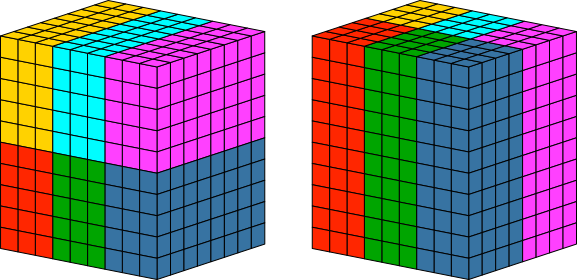
Abb. 5.9: 8×9×10

Für ungerades n (also die mittlere Zahl ungerade) gibt es zwei Lösungen, für gerades n eine Lösung. Dies folgt aus der Teilbarkeit durch 2 und 3 der drei Kantenlängen.