Hans Walser, [20160905]
Fastpythagoreische Dreiecke
Anregung: Heinz Klaus Strick, Leverkusen
1 Worum es geht
Wir suchen natźrliche Zahlen a ˛ b < c so dass die Differenz a2 + b2 – c2 ăkleinŇ ist. Wenn diese Differenz verschwindet, haben wir ein pythagoreisches Tripel. Wenn sie nicht verschwindet, aber ăkleinŇ ist, haben wir ein fastpythagoreisches Tripel. Wir kšnnen damit ein rechtwinkliges Dreieck hinmogeln, das dem Satz des Pythagoras zu widersprechen scheint.
2 Tabelle
In der Tabelle 1 sind die teilerfremden fastpythagoreischen Tripel mit 0 < c ˛ 50 aufgelistet, bei denen die Differenz kleiner oder gleich 4 ist.
|
Nr. |
a |
b |
c |
Diff |
|
|
Nr. |
a |
b |
c |
Diff |
|
|
Nr. |
a |
b |
c |
Diff |
|
1 |
1 |
1 |
2 |
-2 |
|
|
38 |
15 |
16 |
22 |
-3 |
|
|
75 |
22 |
31 |
38 |
1 |
|
2 |
1 |
2 |
3 |
-4 |
|
|
39 |
14 |
17 |
22 |
1 |
|
|
76 |
17 |
34 |
38 |
1 |
|
3 |
2 |
2 |
3 |
-1 |
|
|
40 |
11 |
19 |
22 |
-2 |
|
|
77 |
26 |
29 |
39 |
-4 |
|
4 |
2 |
3 |
4 |
-3 |
|
|
41 |
9 |
20 |
22 |
-3 |
|
|
78 |
25 |
30 |
39 |
4 |
|
5 |
3 |
3 |
4 |
2 |
|
|
42 |
13 |
19 |
23 |
1 |
|
|
79 |
19 |
34 |
39 |
-4 |
|
6 |
3 |
4 |
5 |
0 |
|
|
43 |
7 |
22 |
23 |
4 |
|
|
80 |
9 |
38 |
39 |
4 |
|
7 |
3 |
5 |
6 |
-2 |
|
|
44 |
17 |
17 |
24 |
2 |
|
|
81 |
21 |
34 |
40 |
-3 |
|
8 |
5 |
5 |
7 |
1 |
|
|
45 |
7 |
23 |
24 |
2 |
|
|
82 |
9 |
39 |
40 |
2 |
|
9 |
3 |
6 |
7 |
-4 |
|
|
46 |
12 |
22 |
25 |
3 |
|
|
83 |
29 |
29 |
41 |
1 |
|
10 |
4 |
6 |
7 |
3 |
|
|
47 |
10 |
23 |
25 |
4 |
|
|
84 |
28 |
30 |
41 |
3 |
|
11 |
5 |
6 |
8 |
-3 |
|
|
48 |
7 |
24 |
25 |
0 |
|
|
85 |
23 |
34 |
41 |
4 |
|
12 |
4 |
7 |
8 |
1 |
|
|
49 |
12 |
23 |
26 |
-3 |
|
|
86 |
9 |
40 |
41 |
0 |
|
13 |
6 |
7 |
9 |
4 |
|
|
50 |
7 |
25 |
26 |
-2 |
|
|
87 |
26 |
33 |
42 |
1 |
|
14 |
4 |
8 |
9 |
-1 |
|
|
51 |
17 |
21 |
27 |
1 |
|
|
88 |
9 |
41 |
42 |
-2 |
|
15 |
7 |
7 |
10 |
-2 |
|
|
52 |
14 |
23 |
27 |
-4 |
|
|
89 |
25 |
35 |
43 |
1 |
|
16 |
4 |
9 |
10 |
-3 |
|
|
53 |
10 |
25 |
27 |
-4 |
|
|
90 |
22 |
37 |
43 |
4 |
|
17 |
6 |
9 |
11 |
-4 |
|
|
54 |
7 |
26 |
27 |
-4 |
|
|
91 |
18 |
39 |
43 |
-4 |
|
18 |
5 |
10 |
11 |
4 |
|
|
55 |
16 |
23 |
28 |
1 |
|
|
92 |
13 |
41 |
43 |
1 |
|
19 |
8 |
9 |
12 |
1 |
|
|
56 |
20 |
21 |
29 |
0 |
|
|
93 |
9 |
42 |
43 |
-4 |
|
20 |
5 |
11 |
12 |
2 |
|
|
57 |
19 |
22 |
29 |
4 |
|
|
94 |
16 |
41 |
44 |
1 |
|
21 |
7 |
11 |
13 |
1 |
|
|
58 |
13 |
26 |
29 |
4 |
|
|
95 |
13 |
42 |
44 |
-3 |
|
22 |
5 |
12 |
13 |
0 |
|
|
59 |
15 |
26 |
30 |
1 |
|
|
96 |
32 |
33 |
46 |
-3 |
|
23 |
7 |
12 |
14 |
-3 |
|
|
60 |
13 |
27 |
30 |
-2 |
|
|
97 |
31 |
34 |
46 |
1 |
|
24 |
5 |
13 |
14 |
-2 |
|
|
61 |
17 |
26 |
31 |
4 |
|
|
98 |
29 |
37 |
47 |
1 |
|
25 |
10 |
11 |
15 |
-4 |
|
|
62 |
11 |
29 |
31 |
1 |
|
|
99 |
23 |
41 |
47 |
1 |
|
26 |
5 |
14 |
15 |
-4 |
|
|
63 |
8 |
30 |
31 |
3 |
|
|
100 |
21 |
42 |
47 |
-4 |
|
27 |
12 |
12 |
17 |
-1 |
|
|
64 |
20 |
25 |
32 |
1 |
|
|
101 |
19 |
43 |
47 |
1 |
|
28 |
11 |
13 |
17 |
1 |
|
|
65 |
11 |
30 |
32 |
-3 |
|
|
102 |
28 |
39 |
48 |
1 |
|
29 |
8 |
15 |
17 |
0 |
|
|
66 |
8 |
31 |
32 |
1 |
|
|
103 |
25 |
41 |
48 |
2 |
|
30 |
6 |
16 |
17 |
3 |
|
|
67 |
19 |
27 |
33 |
1 |
|
|
104 |
31 |
38 |
49 |
4 |
|
31 |
10 |
15 |
18 |
1 |
|
|
68 |
8 |
32 |
33 |
-1 |
|
|
105 |
17 |
46 |
49 |
4 |
|
32 |
6 |
17 |
18 |
1 |
|
|
69 |
23 |
25 |
34 |
-2 |
|
|
106 |
14 |
47 |
49 |
4 |
|
33 |
13 |
14 |
19 |
4 |
|
|
70 |
14 |
31 |
34 |
1 |
|
|
107 |
10 |
48 |
49 |
3 |
|
34 |
6 |
18 |
19 |
-1 |
|
|
71 |
8 |
33 |
34 |
-3 |
|
|
108 |
17 |
47 |
50 |
-2 |
|
35 |
6 |
19 |
20 |
-3 |
|
|
72 |
18 |
30 |
35 |
-1 |
|
|
109 |
10 |
49 |
50 |
1 |
|
36 |
11 |
18 |
21 |
4 |
|
|
73 |
23 |
29 |
37 |
1 |
|
|
|
|
|
|
|
|
37 |
9 |
19 |
21 |
1 |
|
|
74 |
12 |
35 |
37 |
0 |
|
|
|
|
|
|
|
Tab. 1: Fastpythagoreische Tripel
3 Gezinkte rechtwinklige Dreiecke
Interessant sind die Beispiele mit einer Differenz ±1. Wir haben ein kleines Rasterquadrat zu viel oder zu wenig. Dieses differierende Rasterquadrat ist in den folgenden Beispielen jeweils gelb markiert.
Zu den Beispielen gibt es noch andere Lšsungen.
3.1 Beispiel Nr. 3
Woher kommt das gelbe Quadrat?
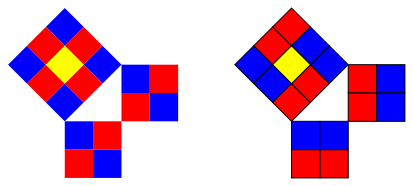
Nr. 3
3.2 Beispiel Nr. 8
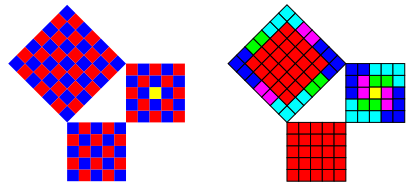
Nr. 8
3.3 Beispiel Nr. 12

Nr. 12
3.4 Beispiel Nr. 14

Nr. 14
3.5 Beispiel Nr. 19

Nr.19
3.6 Beispiel Nr. 21
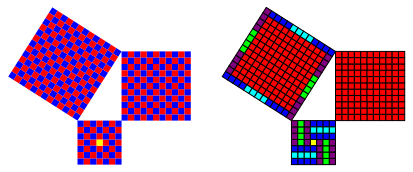
Nr. 21
3.7 Beispiel Nr. 27

Nr. 27
3.8 Beispiel Nr. 28

Nr. 28
3.9 Beispiel Nr. 31
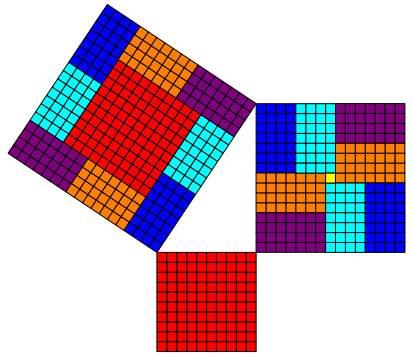
Nr. 31
3.10 Beispiel Nr. 32
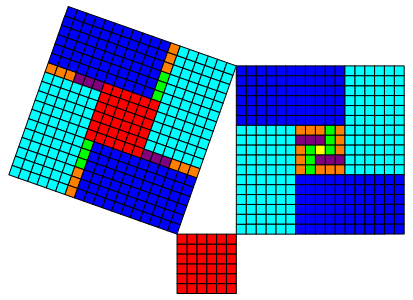
Nr. 32
Websites
Walser: Verschwundenes Quadrat (06.09.2016):
www.walser-h-m.ch/hans/Miniaturen/V/Verschwundenes_Quadrat/Verschwundenes_Quadrat.htm