Hans Walser, [20160913]
Feuerbach-Kreis
Anregung: Manfred Schmelzer, Regensburg
1 Problemstellung
Ein beliebiges Dreieck wird in ein orthogonales Raster eingepasst. Die Abbildung 1 zeigt fźr dasselbe Dreieck die papierrandparallele und eine allgemeine Einpassung.
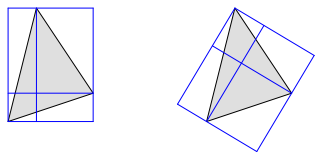
Abb. 1: Dreieck in orthogonalem Raster
Jede Dreiecksseite ist nun Diagonale eines Rechtecks.
Was ist mit den drei anderen Diagonalen (Gegendiagonalen) der drei Rechtecke los?
2 Ergebnis
Die drei anderen Diagonalen (Gegendiagonalen) sind kopunktal, der gemeinsame Schnittpunkt liegt auf dem Feuerbach-Kreis des Dreiecks (Abb. 2).
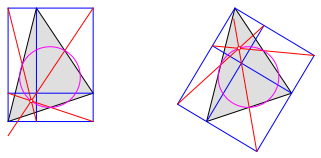
Abb. 2: Gemeinsamer Schnittpunkt auf Feuerbach-Kreis
3 Beweis
Der Beweis geht mit Winkelźberlegungen (Abb. 3 und 4 fźr den nicht speziellen Fall). Die beiden violetten Dreiecke der Abbildung 3 sind Šhnlich. Daher sind die grau markierten Winkel gleich.
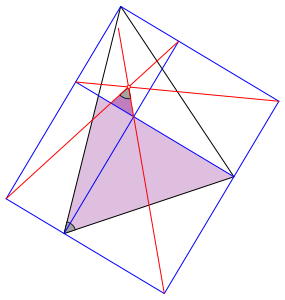
Abb. 3: Gleiche Winkel
Die Abbildung 4 bringt nun die eigentliche Beweisfigur.
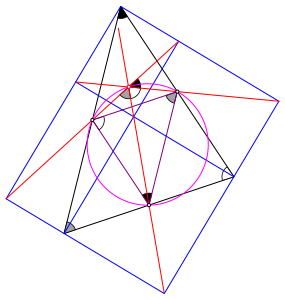
Abb. 4: Beweisfigur
Die in jeweils gleicher Farbe markierten Winkel sind gleich gro§. Die Schnittpunkte von jeweils zwei der drei roten Gegendiagonalen sind auf einem Ortsbogen, die drei Ortsbšgen liegen aber auf dem Umkreis des Seitenmittendreieckes. Dies ist der Feuerbach-Kreis.