1 Worum geht es?

Eine mir bislang unbekannte Eigenschaft des Feuerbach-Kreises (Neunpunkte-Kreis)

Schnittpunkt von vier Euler-Geraden

2 Erinnerung

Der Feuerbach-Kreis kann zum Beispiel definiert werden als der Kreis durch die drei Seitenmitten eines Dreieckes (Abb. 1).

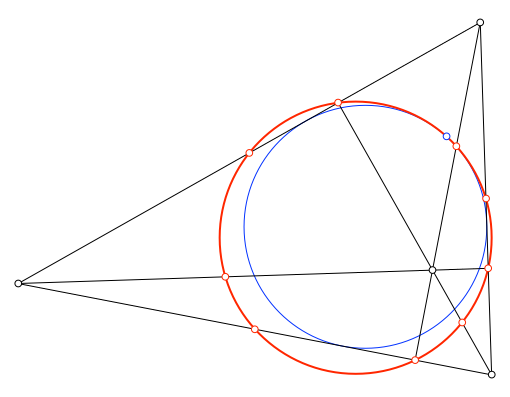
Abb. 1: Feuerbach-Kreis

Der Feuerbach-Kreis verläuft dann auch durch die drei Höhenfußpunkte des Dreieckes (Euler).

Ebenso verläuft der Feuerbach-Kreis durch die Mittelpunkte der Höhenabschnitte vom Höhenschnittpunkt zu den Dreiecksecken. Daher der Name Neunpunkte-Kreis.

Der Feuerbach-Kreis berührt den Inkreis und die drei Ankreise des Dreieckes (Satz von Feuerbach).

Der Mittelpunkt des Feuerbachkreises liegt auf der Euler-Geraden.

3 Unterteilung durch die Höhen

Wir unterteilen das Dreieck durch die Höhen in drei Teildreiecke (Abb. 2) und zeichnen in jedem Teildreieck den Inkreis.

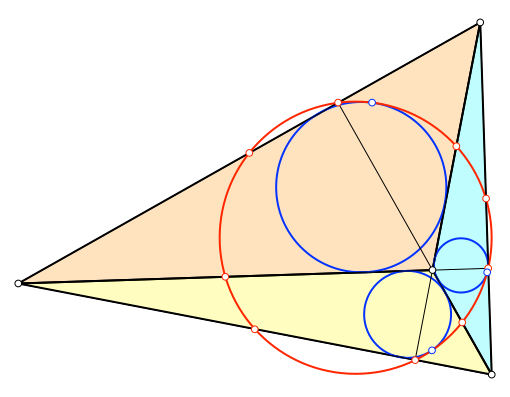
Abb. 2: Teildreiecke

Der Feuerbach-Kreis berührt jeden Inkreis der Teildreiecke.

4 Beweis

Das gelbe Teildreieck der Abbildung 2 ist begrenzt von einer Dreiecksseite und zwei Höhenabschnitten des Startdreieckes. Der Feuerbach-Kreis des Startdreieckes läuft durch die Mittelpunkte dieser drei Strecken, ist also auch der Feuerbach-Kreis des gelben Teildreieckes und berührt nach dem Satz von Feuerbach dessen Inkreis. — Entsprechend für die beiden anderen Teildreiecke.

5 Ankreise der Teildreiecke

Nach dem Satz von Feuerbach berühren nun auch die Ankreise der Teildreiecke den Feuerbach-Kreis. Die Abbildung 3 zeigt die Situation für das orange Teildreieck.

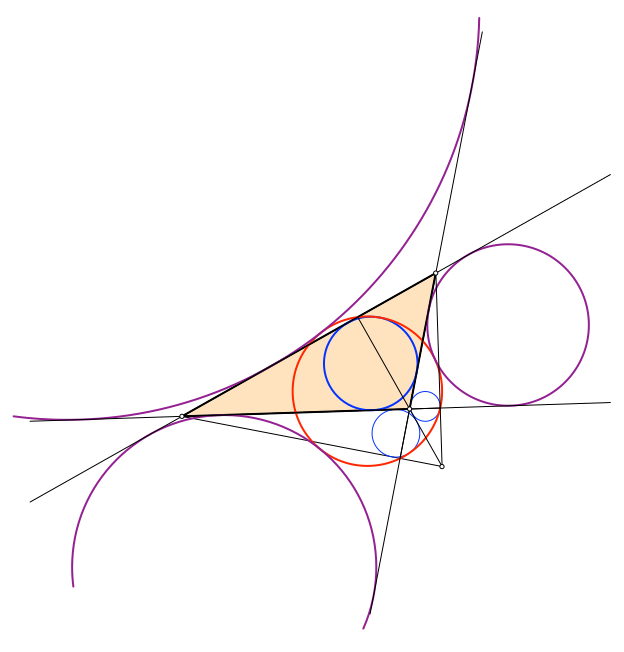
Abb. 3: Ankreise

Somit berührt der Feuerbach-Kreis den Inkreis und die drei Ankreise des Startdreieckes wie auch eines jeden Teildreieckes, insgesamt also 16 Kreise.

6 Kopunktale Euler-Geraden

Der Mittelpunkt des Feuerbach-Kreises liegt auf der Euler-Geraden. Da wir vier Dreiecke (Startdreieck und drei Teildreiecke) mit demselben Feuerbach-Kreis haben, verlaufen deren vier Euler-Geraden durch denselben Punkt, den Mittelpunkt des Feuerbach-Kreises (Abb. 4). Die Euler-Geraden verlaufen auch durch die Höhenschnittpunkte. Dabei sind die Ecken des Startdreieckes jeweils der Höhenschnittpunkt des gegenüberliegenden Teildreieckes.

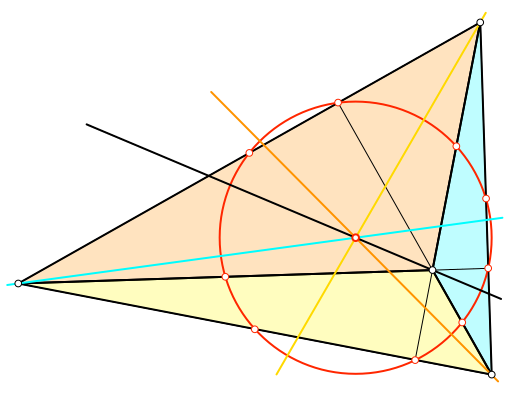
Abb. 4: Die vier Euler-Geraden

Weblinks

Hans Walser: Feuerbach-Elfpunkte-Hyperbeln

http://www.walser-h-m.ch/hans/Miniaturen/F/Feuerbach/Hyperbel.htm

Hans Walser: Feuerbach-Kreis

http://www.walser-h-m.ch/hans/Miniaturen/F/Feuerbach2/Feuerbach2.htm