Hans Walser, [20230739]

Feuerbach

1 Worum es geht

Ein Schnittpunkt im Umfeld der Euler-Geraden

Feuerbach-Kreis

Kiepert-Hyperbel

2 Das Dreieck

Im Dreieck △₄ mit den Ecken A₁A₂A₃ sei A₄ der Höhenschnittpunkt (Abb. 1).

Abb. 1: Dreieck und Höhen

Dann gilt:

Das Dreieck △₁ mit den Ecken A₂A₃A₄ hat den Höhenschnittpunkt A₁.
Das Dreieck △₂ mit den Ecken A₁A₃A₄ hat den Höhenschnittpunkt A₂.

Das Dreieck △₃ mit den Ecken A₁A₂A₄ hat den Höhenschnittpunkt A₃.

Es ist also immer der fehlende Punkt der Höhenschnittpunkt.

3 Euler-Geraden

Nun sei e_j die Euler-Gerade des Dreieckes △_j, j ∈ {1, 2, 3, 4} (Abb. 2).

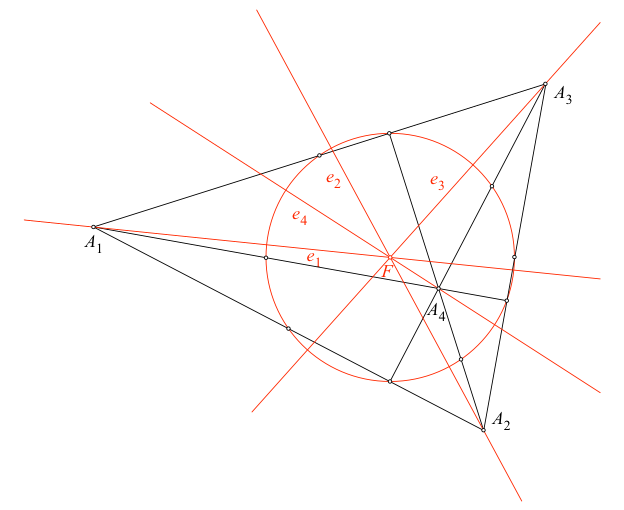
Abb. 2: Euler-Geraden und Feuerbach-Kreis

Dann gilt:

Die Euler-Gerade e_j verläuft durch den Punkt A_j, j ∈ {1, 2, 3, 4}.

Die vier Euler-Geraden e_j, j ∈ {1, 2, 3, 4}, schneiden sich in einem gemeinsamen Punkt F.

Die vier Dreiecke haben einen gemeinsamen Feuerbach-Kreis (auch als Neunpunktekreis bekannt) f. Das Zentrum von f ist F.

4 Schwerpunkte

Weiter sei S_j der Schwerpunkt des Dreieckes △_j, j ∈ {1, 2, 3, 4} (Abb. 3).

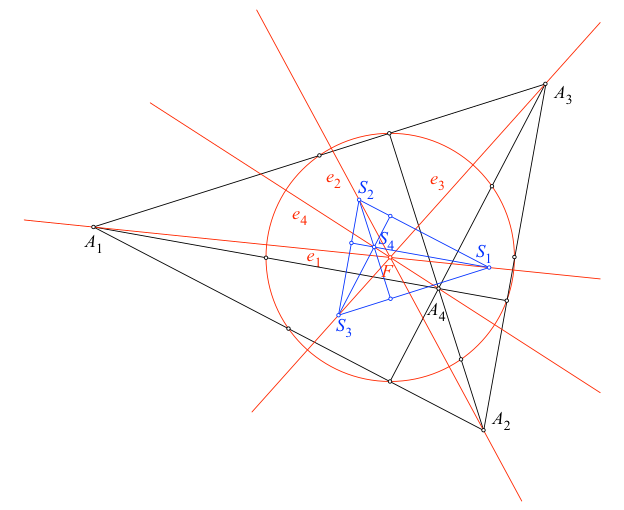
Abb. 3: Schwerpunkte

Dann gilt: Die Konfiguration S₁S₂S₃S₄ ist perspektivähnlich zur Konfiguration A₁A₂A₃A₄. Das Perspektivitätszentrum ist der Punkt F. Der Perspektivitätsfaktor ist –⅓.

5 Kiepert-Hyperbeln

Die Kiepert-Hyperbel eines Dreieckes ist der Kegelschnitt durch die drei Ecken des Dreieckes und dessen Höhenschnittpunkt und sowie den Schwerpunkt. Der Mittelpunkt der Kiepert-Hyperbel liegt auf dem Feuerbachkreis (Neunpunktekreis) des Dreieckes.

Nun sei k_j die Kiepert-Hyperbel des Dreieckes △_j, j ∈ {1, 2, 3, 4} (Abb. 4).

Abb. 4: Kiepert-Hyperbeln

Dann gilt: Durch jeden Punkt A_j, j ∈ {1, 2, 3, 4}, verlaufen alle vier Kiepert-Hyperbeln. Die Kiepert-Hyperbel k_j verläuft durch S_j.

Weiter sei K_j der Mittelpunkt der Kiepert-Hyperbel k_j des Dreieckes △_j, j ∈ {1, 2, 3, 4}. Die vier Mittelpunkte K_j, j ∈ {1, 2, 3, 4}, liegen auf dem Feuerbachkreis f.

6 Schritt für Schritt

Die Abbildung 5 zeigt das schrittweise Vorgehen.

Abb. 5: Schritt für Schritt

7 Beweis

Die Höhenfußpunkte der vier Dreiecke △_j, j ∈ {1, 2, 3, 4} fallen zusammen. Daher haben die vier Dreiecke einen gemeinsamen Feuerbachkreis. Das Teilverhältnis von Schwerpunkt, Zentrum des Feuerbachkreises und Höhenschnittpunkt auf der Eulergeraden eines Dreieckes ist 1:3. Daher die Perspektivähnlichkeit der Konfiguration S₁S₂S₃S₄ mit der Konfiguration A₁A₂A₃A₄.

Weblinks

Hans Walser: Feuerbachse Elfpunkgte-Hyperbeln

http://www.walser-h-m.ch/hans/Miniaturen/F/Feuerbach/Hyperbel.htm

Hans Walser: Feuerbach-Kreis

http://www.walser-h-m.ch/hans/Miniaturen/F/Feuerbach2/Feuerbach2.htm

Hans Walser: Feuerbach-Kreis

http://www.walser-h-m.ch/hans/Miniaturen/F/Feuerbach3/Feuerbach3.html