Hans Walser, [20150521]
Fibonacci-10-Ecke
Wir
bilden gleichschenklige Dreiecke mit der Basis 
und der
SchenkellŠnge 
, wobei 
die
źblichen Fibonacci-Zahlen sind.
10
solcher Dreiecke suchen wir zu einem Zehneck zusammenzufźgen. Dieses schlie§t
sich aber nicht ganz. Die Abbildung 1 zeigt die Situation fźr die
Fibonacci-Zahlen 
und 
.
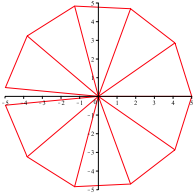
Abb. 1: 3 und 5
Die folgenden Abbildungen zeigen der Reihe nach die Figuren fźr die Folge der Fibonacci-Zahlen. Wir haben im Wechsel źberschie§ende und lźckenhafte Figuren.
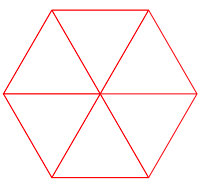
Abb. 2: 1 und 1
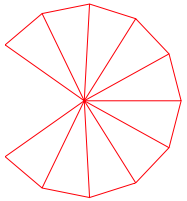
Abb. 3: 1 und 2
Abb. 4: 2 und 3
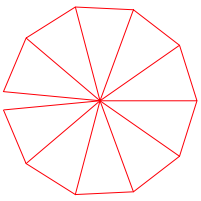
Abb. 5: 3 und 5
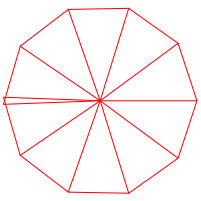
Abb. 6: 5 und 8
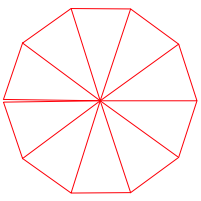
Abb. 7: 8 und 13
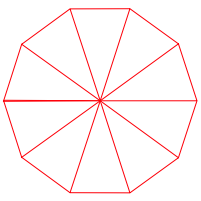
Abb. 8: 13 und 21
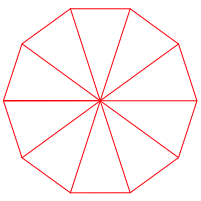
Abb. 9: 21 und 34
Die Figuren nŠhern sich immer mehr dem regulŠren Zehneck an.