Hans Walser, [20100514a]

Fibonacci trifft Pythagoras

Anregung: I. Y.

1 Worum geht es?

Mit den Fibonacci-Zahlen werden pythagoreische Dreiecke konstruiert, die im Limes zu den Fibonacci-Zahlen zurückführen. Als Nebenresultat ergibt sich eine Folge von Konstruktionen für den goldenen Schnitt.

2 Pythagoreische Dreiecke

Erinnerung: Mit erhalten wir durch

ein ganzzahliges Zahlentripel, welches der Bedingung genügt. Damit können wir auch ein rechtwinkliges Dreieck mit ganzzahligen Seitenlängen konstruieren.

Wir verwenden nun für u und v die Fibonacci-Zahlen der folgenden Tabelle. Diese haben die Startwerte und die Rekursion . In der Tabelle sind auf Vorrat auch noch die Lucas-Zahlen aufgelistet, welche sich von den Fibonacci-Zahlen nur durch andere Startwerte unterscheiden. Die Rekursion ist dieselbe.

2.1 Versatz 1

In der folgenden Tabelle sind für u und v die Fibonacci-Zahlen mit einem Versatz von 1 verwendet worden, das heißt es ist und . Die u sind gegenüber den v um eine Stelle versetzt.

1	2	1	3	4	5	0.750000	1.250000
2	3	2	5	12	13	0.416667	1.083333
3	5	3	16	30	34	0.533333	1.133333
4	8	5	39	80	89	0.487500	1.112500
5	13	8	105	208	233	0.504808	1.120192
6	21	13	272	546	610	0.498168	1.117216
7	34	21	715	1428	1597	0.500700	1.118347
8	55	34	1869	3740	4181	0.499733	1.117914
9	89	55	4896	9790	10946	0.500102	1.118080
10	144	89	12815	25632	28657	0.499961	1.118017
11	233	144	33553	67104	75025	0.500015	1.118041
12	377	233	87840	175682	196418	0.499994	1.118031
13	610	377	229971	459940	514229	0.500002	1.118035
14	987	610	602069	1204140	1346269	0.499999	1.118034
15	1597	987	1576240	3152478	3524578	0.500000	1.118034

Wir vermuten auf Grund dieser Tabelle:

Für nehmen die pythagoreischen Dreiecke das Seitenverhältnis

an. Das ist das klassische rechtwinklige Dreieck, das sehr vielen Konstruktionen des goldenen Schnittes zugrunde liegt.

2.2 Versatz 2

Nun ist und . Die u sind gegenüber den v um zwei Stellen versetzt, die v bleiben unverändert.

1	3	1	8	6	10	1.333333	1.666667
2	5	2	21	20	29	1.050000	1.450000
3	8	3	55	48	73	1.145833	1.520833
4	13	5	144	130	194	1.107692	1.492308
5	21	8	377	336	505	1.122024	1.502976
6	34	13	987	884	1325	1.116516	1.498869
7	55	21	2584	2310	3466	1.118615	1.500433
8	89	34	6765	6052	9077	1.117812	1.499835
9	144	55	17711	15840	23761	1.118119	1.500063
10	233	89	46368	41474	62210	1.118002	1.499976

Wir vermuten auf Grund dieser Tabelle:

Für nehmen die pythagoreischen Dreiecke das Seitenverhältnis

an.

2.3 Versatz 5

Noch das Beispiel mit Versatz 5, also .

1	13	1	168	26	170	6.461538	6.538462
2	21	2	437	84	445	5.202381	5.297619
3	34	3	1147	204	1165	5.622549	5.710784
4	55	5	3000	550	3050	5.454545	5.545455
5	89	8	7857	1424	7985	5.517556	5.607444
6	144	13	20567	3744	20905	5.493323	5.583600
7	233	21	53848	9786	54730	5.502555	5.592683
8	377	34	140973	25636	143285	5.499025	5.589210
9	610	55	369075	67100	375125	5.500373	5.590537
10	987	89	966248	175686	982090	5.499858	5.590030

Wir vermuten:

Für nehmen die pythagoreischen Dreiecke das Seitenverhältnis

an. Ob sich auch mit diesem Dreieck der goldene Schnitt konstruieren lässt, überlassen wir den Tüftlern.

3 Übersicht

Ein Feldversuch mit verschiedenen Versatzzahlen m lässt mit der Normierung folgende Seitenverhältnisse für die jeweiligen Grenzdreiecke vermuten:

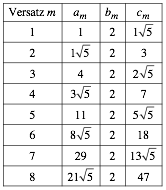
Wir erkennen bei den a und c im Wechsel die Lucas-Zahlen und die Fibonacci-Zahlen. Wir vermuten somit:

m ungerade:

m gerade:

4 Beweise

4.1 Schreibweisen und Formeln

Für den goldenen Schnitt verwenden wir die Schreibweisen:

Es ist .

Ferner verwenden wir die Formeln von Binet:

Wegen ist ; wir können bei Grenzwertprozessen den weglassen.

Schließlich die Formel von Catalan:

Mit und lässt sich diese Formel von Catalan in folgender Form schreiben:

4.2 Grenzdreiecke

Wir zeigen zunächst:

Für ungerades m erhalten wir unter Verwendung von :

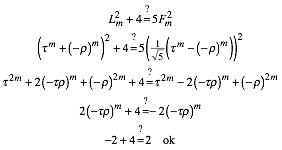
Für gerades m verläuft die Rechnung analog.

4.3 Grenzwerte

Zu zeigen ist:

m ungerade:

m gerade:

Wegen der oben bewiesenen Pythagoras-Beziehung haben wir in jedem der beiden Fälle nur einen der beiden Grenzwerte nachzuweisen.

Zunächst sei wiederum m ungerade. Die Formel von Catalan lautet in diesem Fall:

Aufgrund der Formeln für die Konstruktion der pythagoreischen Dreiecke erhalten wir damit:

Weiter ist:

Damit erhalten wir:

Damit ist der Fall für ungerades m vollständig bewiesen.

Für gerades m läuft der Beweis analog, es wird bewiesen.

5 Konstruktionen des goldenen Schnittes im Quadratraster

Aufgrund der Tabelle

ergibt sich eine Folge von Konstruktionen des goldenen Schnittes im Quadratraster, allerdings mit einer Fallunterscheidung bezüglich der Parität von m.

In beiden Fällen beginnen wir mit einem Rechteck im Karoraster, das Einheiten lang und 2 Einheiten hoch ist.

Für ungerades m arbeiten wir dann gemäß Figur (Figur exakt für ). Am oberen Rand wird durch Dritteln die Fiboancci-Zahl sichtbar gemacht. Am unteren Rand tragen wir von rechts her den Abstand ein. Dann schlagen wir einen Bogen um die Ecke rechts oben gemäß Figur und erhalten auf dem oberen Rand einen Teilpunkt, welcher das aus den ersten beiden Fibonacci-Strecken gebildete Intervall im Verhältnis des goldenen Schnittes teilt. Der Kreisbogen verläuft von unten nach oben.

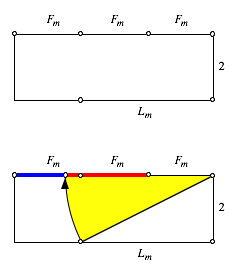
m ungerade

Die blaue und die rote Strecke sind dann im Verhältnis des goldenen Schnittes.

Für gerades m sieht das so aus (Figur exakt für ). Nun werden die drei Fibonacci-Strecken am unteren Rand eingezeichnet und am oberen Rand von rechts her abgetragen. Der Kreisbogen hat immer noch die Ecke rechts oben als Zentrum, verläuft nun aber von oben nach unten.

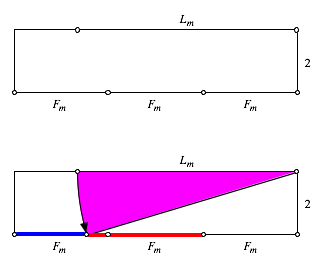
m gerade

Nun explizite Beispiele.

5.1 m = 1

Es ist .

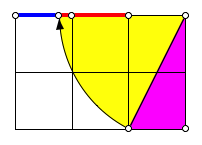
m = 1

5.2 m = 2

Es ist .

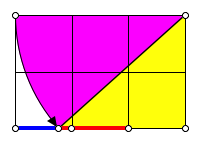
m = 2

5.3 m = 3

Es ist .

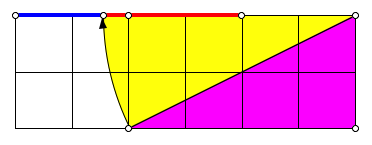
m = 3

5.4 m = 4

Es ist .

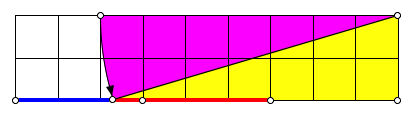
m = 4

5.5 m = 5

Es ist .

m = 5