Hans Walser, [20120628], [20140317a]
Fibonacci-Dreieck
Anregung: K. H., Gš.
1 Fragestellung
Ein rechtwinkliges
Dreieck habe als KathetenlŠngen die Fibonacci-Zahlen 
und 
. Wie lang ist seine Hypotenuse.
2 Beispiele
|
n |
|
|
Hypotenuse |
Bemerkungen |
|
1 |
1 |
1 |
|
Halbes Quadrat |
|
2 |
1 |
2 |
|
Domino-Dreieck oder |
|
3 |
2 |
3 |
|
|
|
4 |
3 |
5 |
|
|
Wir erkennen die bekannte Formel:
Illustration im Fibonacci-Dreieck:
Fibonacci-Dreieck
3 Beweis
Es sei 
(goldener
Schnitt). Wir verwenden die Formel von Binet:
Damit wird:
Entsprechend:
Damit erhalten wir:
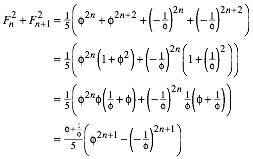
Wegen 
folgt
schlie§lich:
Dies war zu beweisen.
4 Normierung
Wir normieren die lange
Kathete auf 1, indem wir alle LŠngen durch 
dividieren.
Normierung
5 Konstruktion
Und nun fŸhren wir eine
Konstruktion durch, die wir der klassischen Konstruktion des Goldenen Schnittes
abgeguckt haben. FŸr 
ist es genau die
klassische Konstruktion des Goldenen Schnittes (vgl. Walser, 2013).
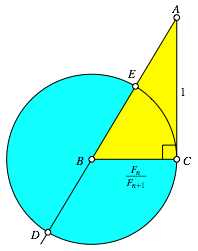
Konstruktion
Wir fŸhren folgende Zahlen ein:
Die Tabelle zeigt die ersten Werte dieser Zahlen.
|
|
|
|
|
1 |
2.414213562 |
0.4142135624 |
|
2 |
1.618033989 |
0.6180339887 |
|
3 |
1.868517092 |
0.5351837585 |
|
4 |
1.766190379 |
0.566190379 |
|
5 |
1.804247642 |
0.5542476415 |
|
6 |
1.789564425 |
0.558795194 |
|
7 |
1.795151337 |
0.5570560986 |
|
8 |
1.793014188 |
0.5577200707 |
|
9 |
1.793830048 |
0.5574664117 |
|
10 |
1.793518351 |
0.5575632944 |
|
11 |
1.793637399 |
0.5575262875 |
|
12 |
1.793591925 |
0.5575404227 |
|
13 |
1.793609294 |
0.5575350235 |
|
14 |
1.79360266 |
0.5575370858 |
|
15 |
1.793605194 |
0.5575362981 |
|
16 |
1.793604226 |
0.557536599 |
|
17 |
1.793604596 |
0.5575364841 |
|
18 |
1.793604454 |
0.557536528 |
|
19 |
1.793604508 |
0.5575365112 |
|
20 |
1.793604488 |
0.5575365176 |
|
21 |
1.793604496 |
0.5575365152 |
|
22 |
1.793604493 |
0.5575365161 |
|
23 |
1.793604494 |
0.5575365157 |
|
24 |
1.793604493 |
0.5575365159 |
|
25 |
1.793604493 |
0.5575365158 |
|
26 |
1.793604493 |
0.5575365158 |
|
27 |
1.793604493 |
0.5575365158 |
|
28 |
1.793604493 |
0.5575365158 |
|
29 |
1.793604493 |
0.5575365158 |
|
30 |
1.793604493 |
0.5575365158 |
Tabelle
6 Eigenschaften der Zahlen
FŸr das Produkt der beiden Zahlen erhalten wir:
Wegen 
ist 
und daher:
Die beiden Zahlen sind Kehrwerte voneinander.
FŸr die Differenz der beiden Zahlen erhalten wir:
Die Differenzen sind rational.
7 SonderfŠlle
FŸr 
erhalten wir: 
FŸr 
erhalten wir den
Goldenen Schnitt: 
FŸr 
wird das Dreieck
das halbe Goldene Rechteck mit der Langseite 1 und der Schmalseite 
. Wir erhalten:
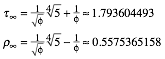
Literatur
Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.