Hans Walser, [20150825]
Fibonacci-Dreieck
1 Worum geht es
Es wird ein Zahlendreieck hergeleitet, das viele Beziehungen zur Fibonacci-Folge hat.
2 Funktionenfolge
Mit 
bezeichnen
wir den Goldenen Schnitt (Walser 2013):
(1)
Nun definieren wir eine Funktionenfolge:
(2)
Erste Beispiele:
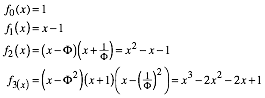(3)
Im Folgenden die Beispiele fźr n = 0 ... 8.
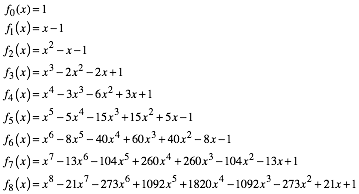(4)
Die Koeffizientenmatrix ist eine Dreiecksmatrix (Tab. 1).
|
1 |
|
|
|
|
|
|
|
|
|
1 |
–1 |
|
|
|
|
|
|
|
|
1 |
–1 |
–1 |
|
|
|
|
|
|
|
1 |
–2 |
–2 |
1 |
|
|
|
|
|
|
1 |
–3 |
–6 |
3 |
1 |
|
|
|
|
|
1 |
–5 |
–15 |
15 |
5 |
–1 |
|
|
|
|
1 |
–8 |
–40 |
60 |
40 |
–8 |
–1 |
|
|
|
1 |
–13 |
–104 |
260 |
260 |
–104 |
–13 |
1 |
|
|
1 |
–21 |
–273 |
1092 |
1820 |
–1092 |
–273 |
21 |
1 |
Tab. 1: Dreiecksmatrix
Es handelt sich dabei um das Fibonacci-Dreieck (Signed Fibonomial triangle, oeis.org/A055870).
In der zweiten Spalte erkennen wir (bis auf Vorzeichen) die Fibonacci-Zahlen.
In der dritten Spalte haben wir (bis auf Vorzeichen) die FlŠcheninhalte der Fibonacci-Rechtecke gemŠ§ Abbildung 1.
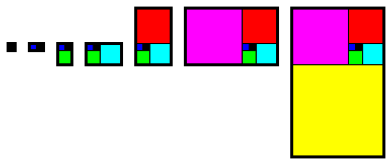
Abb. 1: Fibonacci-Rechtecke
Die Zeilen geben im Prinzip die Rekursionskoeffizienten fźr die Potenzen der Fibonacci-Zahlen. So ist zum Beispiel:
(5)
Die Abbildung 2 zeigt das Fibonacci-Dreieck in einer nostalgischen Anordnung.
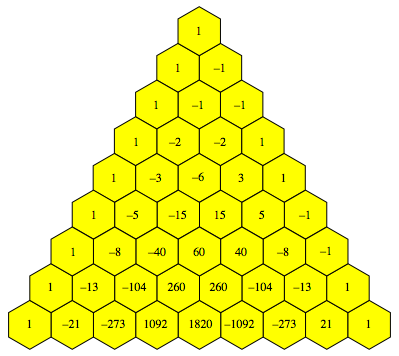
Abb. 2: Fibonacci-Dreieck
Das Dreieck ist bis auf Vorzeichen axialsymmetrisch.
3 Funktionsgrafen
Die
Abbildung 3 zeigt die Funktionsgrafen und die Nullstellen fźr 
.
Abb. 3: Funktionsgrafen
4 Berechnung der Elemente
Die
Elemente 
des
Fibonacci-Dreiecks kšnnen wie folgt berechnet werden (
bezeichnet
die Fibonacci-Zahlen):
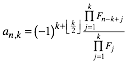(6)
Websites
Signed Fibonomial triangle: oeis.org/A055870
Triangle of Fibonomial coefficients: oeis.org/A010048
Literatur
Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.