Hans Walser, [20141023]
Fibonacci-Intervalle
0 Worum geht es?
Es werden zwei Beispiele von Algorithmen angegeben, welche zu den Fibonacci-Zahlen und zum Goldenen Schnitt fŸhren.
1 BrŸche
1.1 Startintervall
Wir
beginnen mit dem offenen Intervall 
.
1.2 Nenner 2
In diesem
offenen Intervall 
ist 
der einzige Bruch mit dem Nenner 2.
Nun
verkleinern wir das Intervall auf 
.
1.3 Nenner 3
In diesem
offenen Intervall ist 
der einzige Bruch mit dem Nenner 3. Der
Bruch 
ist zu klein.
Nun
verkleinern wir das Intervall auf 
.
1.4 Nenner 4
Dieses
offene Intervall enthŠlt keinen Bruch mit dem Nenner 4. Der Bruch 
ist gerade noch zu klein, der Bruch 
zu gro§.
1.5 Nenner 5
Hingegen
enthŠlt das Intervall den Bruch 
als einzigen Bruch mit dem Nenner 5.
Nun
verkleinern wir das Intervall auf 
.
Wir nehmen den ãneuenÒ Bruch als die eine und den neuen Bruch des
vorangegangenen Schrittes als die andere Grenze.
1.6 Nenner 6
Wegen 
einerseits und 
enthŠlt dieses Intervall keinen Bruch mit
dem Nenner 6.
1.7 Nenner 7
Wegen 
und 
enthŠlt dieses Intervall auch keinen
Bruch mit dem Nenner 7.
1.8 Nenner 8
Bei
BrŸchen mit dem Nenner 8 werden wir wieder fŸndig. Es ist 
, 
und 
.
Damit ist 
der einzige Bruch mit Nenner 8 im
Intervall.
Nun
verkleinern wir das Intervall auf 
.
1.9 Nenner 9
Wegen 
und 
enthŠlt
das Intervall keinen Bruch mit dem Nenner 9.
1.10 Nenner 10
Wegen 
und 
enthŠlt
das Intervall keinen Bruch mit dem Nenner 10.
1.11 Nenner 11
Wegen 
und 
enthŠlt
das Intervall keinen Bruch mit dem Nenner 11.
1.12 Nenner 12
Wegen 
und 
enthŠlt
das Intervall keinen Bruch mit dem Nenner 12.
1.13 Nenner 13
Bei
BrŸchen mit dem Nenner 13 werden wir wieder fŸndig. Es ist 
, 
und 
. Damit ist 
der
einzige Bruch mit Nenner 13 im Intervall.
Nun
verkleinern wir das Intervall auf 
.
1.14 Und so weiter
Offenbar werden wir genau bei BrŸchen fŸndig, deren Nenner Fibonacci-Zahlen sind. Und zu jeder Fibonacci-Zahl gibt es nur einen passenden Bruch mit diesem Nenner. Sein ZŠhler ist die vorangegangene Fibonacci-Zahl.
1.15 Brute Force
Mit dem Programm
N:=1000: #
Obergrenze
a:=1:
b:=1/2:
print(a);
print(b);
for n from 3 to
N do
for k from 1 to n do
if (a < k/n
and k/n < b) or (b <
k/n and k/n < a) then
a:=b: b:=k/n:
print(k/n);
end:
end:
end:
erhalten wir die Ausgabe:
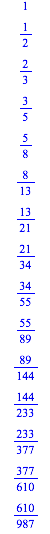
Tab. 1: Fibonacci-Zahlen in BrŸchen
Unsere Vermutung wird bestŠtigt. Beweis? — Der knifflige Punkt ist, zu zeigen, dass andere Zahlen als die Fibonacci-Zahlen nicht in die KrŠnze kommen.
Der
Grenzwert der BrŸche der Tabelle 1 ist der Goldene Schnitt 
.
2 Im Quadratraster
Wir arbeiten im ersten Quadraten eines Quadratrasters (Abb. 1).
Abb. 1: Im ersten Quadranten
Im Innern dieses Quadranten (also nicht auf dem Rand) wŠhlen wir den zum Ursprung (0, 0) nŠchsten Punkt. Dies ist der Punkt (1, 1).
Wir legen nun einen Strahl vom Ursprung aus durch diesen Punkt und definieren einen kleineren Sektor gemŠ§ Abbildung 2.
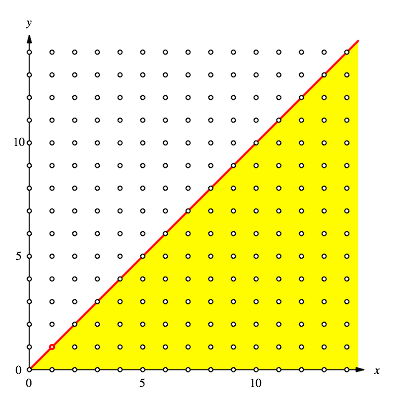
Abb. 2: Verkleinerter Sektor
Im Innern dieses verkleinerten Sektors wŠhlen wir wiederum den zum Ursprung nŠchsten Punkt. Dies ist der Punkt (2, 1).
Wir legen nun einen Strahl vom Ursprung aus durch diesen Punkt und definieren einen noch kleineren Sektor gemŠ§ Abbildung 3.
Die Sektorgrenzen sind jeweils der neue Strahl und der Strahl vom vorhergegangenen Arbeitsschritt.
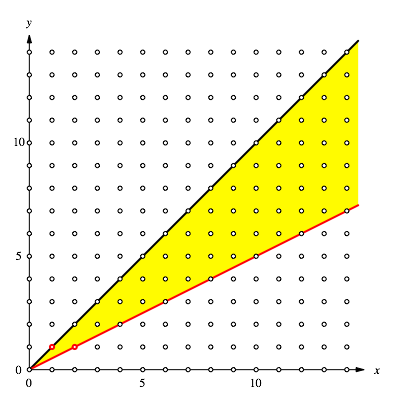
Abb. 3: Erneute Verkleinerung des Sektors
Der zum Ursprung nŠchste Punkt im Innern dieses Sektors ist (3, 2).
Erneut verkleinern wir den Sektor (Abb. 4).
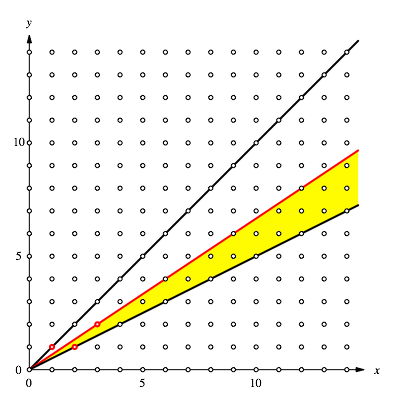
Abb. 4: Weitere Verkleinerung des Sektors
Interessanterweise gibt es nun keinen Punkt mit der x-Koordinate 4 in diesem Sektor. Der Punkt (4, 2) ist auf dem Rand und daher nicht zulŠssig. Der zum Ursprung nŠchste Punkt ist (5, 3).
Die Abbildung 5 zeigt den folgenden Schritt.
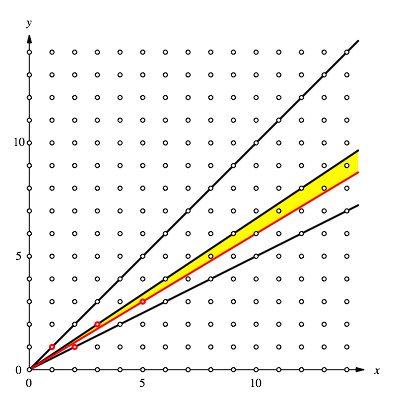
Abb. 5: NŠchster Schritt
FŸr die x-Koordinaten 6 und 7 gibt es keine Punkt im Innern des aktuellen Sektors. Der zum Ursprung nŠchste Punkt ist (8, 5). SpŠtestens hier merkt man, dass die Sache mit den Fibonacci-Zahlen zu tun hat.
Die Abbildung 6 zeigt den Folgeschritt.
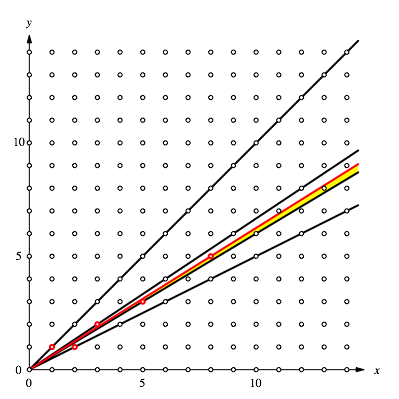
Abb. 6: NŠchster Schritt
FŸr die x-Koordinaten 9, 10, 11 und 12 gibt es keine inneren Punkt im aktuellen Sektor. Der nŠchste Punkt ist (13, 8).
Die Abbildung 7 zeigt, wie es immer enger wird.
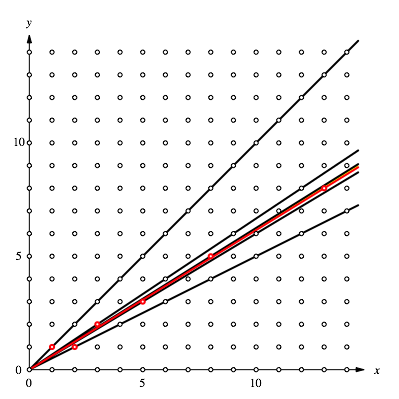
Abb. 7: Enger Sektor
Und so weiter.
Die Strahlen haben der Reihe nach die Steigungen:
Das
entspricht den Werten der Tabelle1. Die Steigungen streben gegen den Goldenen Schnitt 
.
Die jeweils zum Ursprung nŠchsten Punkte sind:
(1, 1), (2, 1), (3, 2), (5, 3), (8, 5), (13, 8), ...
Ihre AbstŠnde vom Ursprung sind der Reihe nach:
Die
Quotienten aufeinanderfolgender AbstŠnde streben gegen den Goldenen Schnitt 
.
Die Radikanden der AbstŠnde sind eine Teilfolge der Fibonacci-Folge, nŠmlich jedes zweite Folgenglied. Sie erfŸllen die Rekursion:
Dies ist eine Verallgemeinerung der Ÿblichen Fibonacci-Rekursion.
Die
Quotienten aufeinanderfolgender Radikanden streben gegen das Quadrat des Goldenen
Schnittes, also 
.