Hans Walser, [20240512]

Fibonacci-Kreisteilung

Idee und Anregung: Jo Niemeyer, Berlin

1 Worum es geht

Unterteilung des Kreises in Sektoren im Verhältnis der Fibonacci-Folge.

Vergleich mit der Unterteilung im Goldenen Schnitt.

2 Beispiel

Wir unterteilen den Kreis in 1 + 1 + 2 + 3 + 5 + 8 = 20 gleiche Sektoren (Abb. 1). Die Summanden sind die ersten sechs Fibonacci-Zahlen.

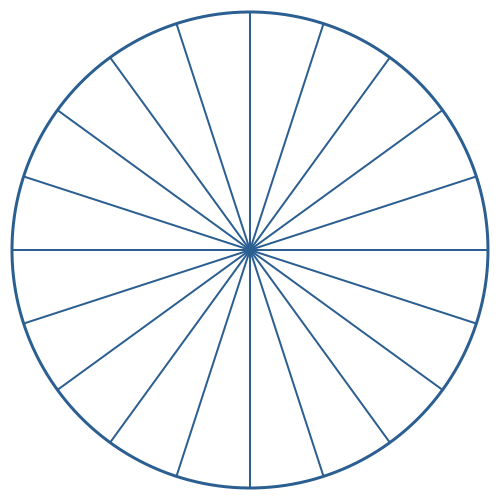
Abb. 1: 20 gleiche Sektoren

Nun gruppieren wir die Sektoren entsprechend der Fibonacci-Zahlen (Abb. 2). Die Anordnung beginnt oben mit einem gelben Sektor und verläuft im Uhrzeigersinn.

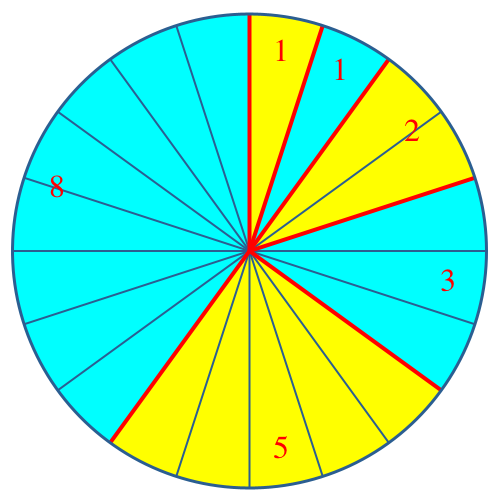
Abb. 2: Gruppierung der ersten sechs Fibonacci-Zahlen

Die Abbildung 3 zeigt die Situation für die Summe der ersten sieben Fibonacci-Zahlen.

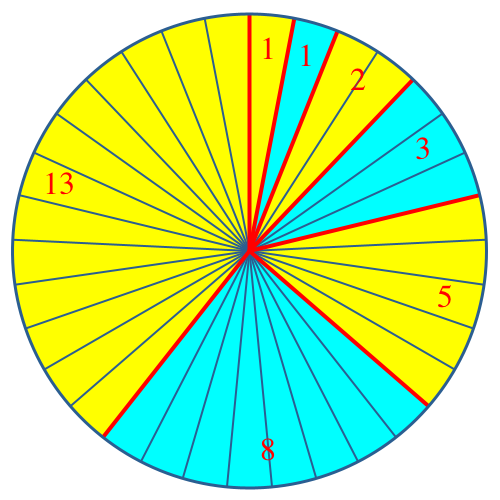
Abb. 3: Die ersten sieben Fibonacci-Zahlen

Der erste Sektor oben rechts, welcher der ersten Fibonacci-Zahl 1 entspricht, ist immer gelb. Der letzte Sektor, welcher der größten vorkommenden Fibonacci-Zahl entspricht, ist im Wechsel hellblau und gelb.

Die Abbildung 4 zeigt der Reihe nach die Situation für die ersten 20 Fibonacci-Zahlen.

Abb. 4: Die ersten 20 Fibonacci-Zahlen

In der Abbildung 5 sind die blauen Trennstriche der ursprünglichen Unterteilung weggelassen. Die roten Trennstriche nähern sich einer Grenzlage.

Abb. 5: Ohne Trennstriche

3 Unterteilung im Goldenen Schnitt

Mit Φ = (1 + √5)/2 ≈1.618 bezeichnen wir den Goldenen Schnitt.

Wir unterteilen nun den Vollkreis im Verhältnis 1:Φ = Φ^–2: Φ^–1. Der kleinere Teil (Minor, gelb in Abb. 6) hat den Anteil Φ^–2 ≈ 38.197%, der größere Teil (Major, weiß in Abb. 6) hat den Anteil Φ^–1 ≈ 61.803%.

Die Anordnung geschieht jetzt im Gegenuhrzeigersinn, und zwar kommt der Minor zuerst.

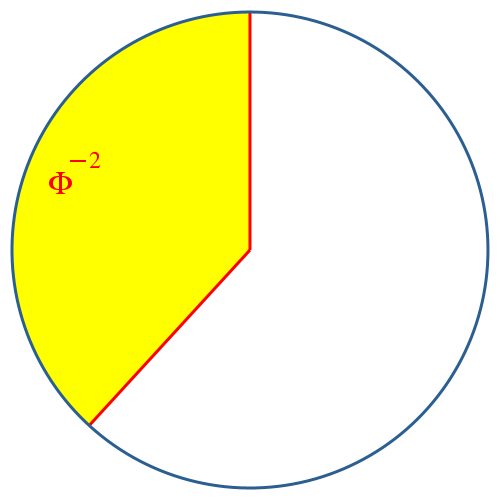
Abb. 6: Unterteilung im Goldenen Schnitt

Nun unterteilen wir den größeren Teil, also den Major, wieder im Verhältnis des Goldenen Schnittes 1:Φ (Abb. 7). Man beachte, dass der Major des Majors (weiß in Abb. 7) gleich groß ist wie der Minor des Ganzen (gelb in Abb. 6 und Abb. 7).

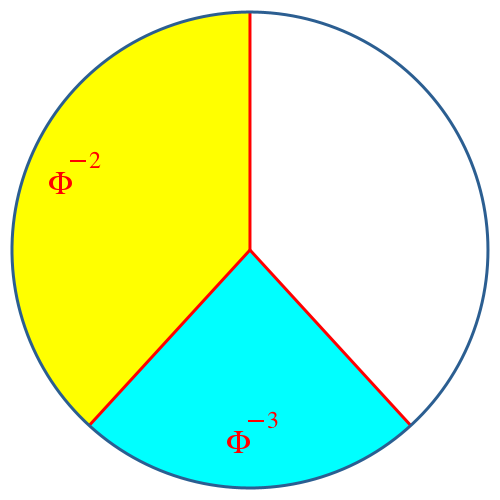
Abb. 7: Zweiter Unterteilungsschritt

Die Abbildungen 8 und 9 zeigen die beiden folgenden Unterteilungsschritte. Der weiße Restsektor ist jeweils gleich groß wie der zweitletzte farbige Sektor.

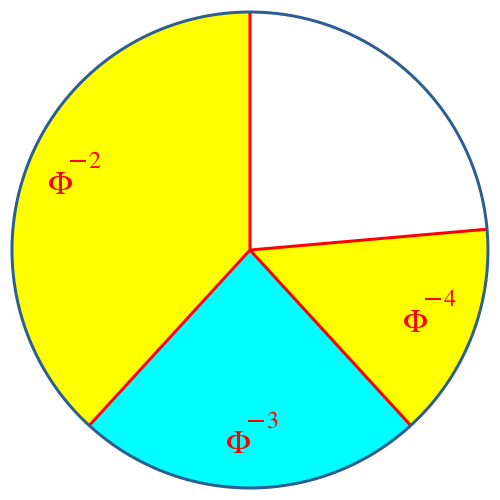
Abb. 8: Dritter Unterteilungsschritt

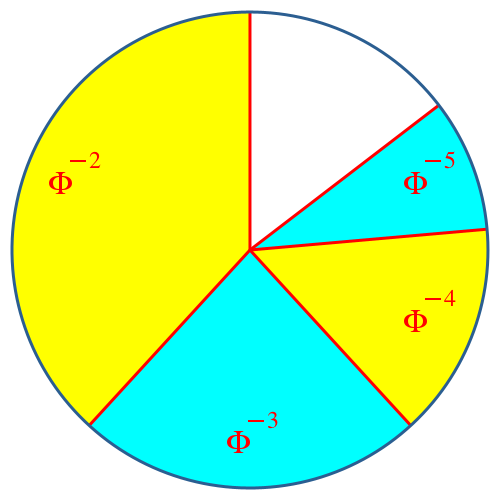
Abb. 9: Vierter Unterteilungsschritt

Und so geht es weiter (Abb. 10).

Abb. 10: Die ersten 20 Unterteilungen

Die Abbildung 10 illustriert folgende Formel:

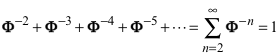
4 Vergleich

Die roten Trennstriche der Abbildungen 5 und 10 sehen „am Ende“, das heißt nach dem Grenzübergang n → ∞, gleich aus.

Literatur

Grevsmühl, Ulrich (1993): 20 Punkte – ein Land-Art Projekt von Jo Niemeyer. Mit einem Beitrag von Eugen Gomringer. Edition Partanen, Schluchsee.

Walser, Hans (2024): Der Goldene Schnitt. Geometrische und zahlentheoretische Betrachtungen. 7. Auflage. Springer Spektrum.
Print-ISBN 978-3-662-68556-3. E-Book_ISBN 978-3-662-68557-0.
https://doi.org/10.1007/978-3-662-68557-0