Hans Walser, [20221221]
Fibonacci-Matrix
1 Worum geht es?
Eine aus verallgemeinerten Fibonacci-Folgen zusammengesetzte Matrix
2 Die Matrix
In der Matrix (Abb. 1) erkennen wir in der ersten Spalte die Verdoppelungs-Folge, in der zweiten Spalte die Fibonacci-Folge. Was ist in den weiterten Spalten los?
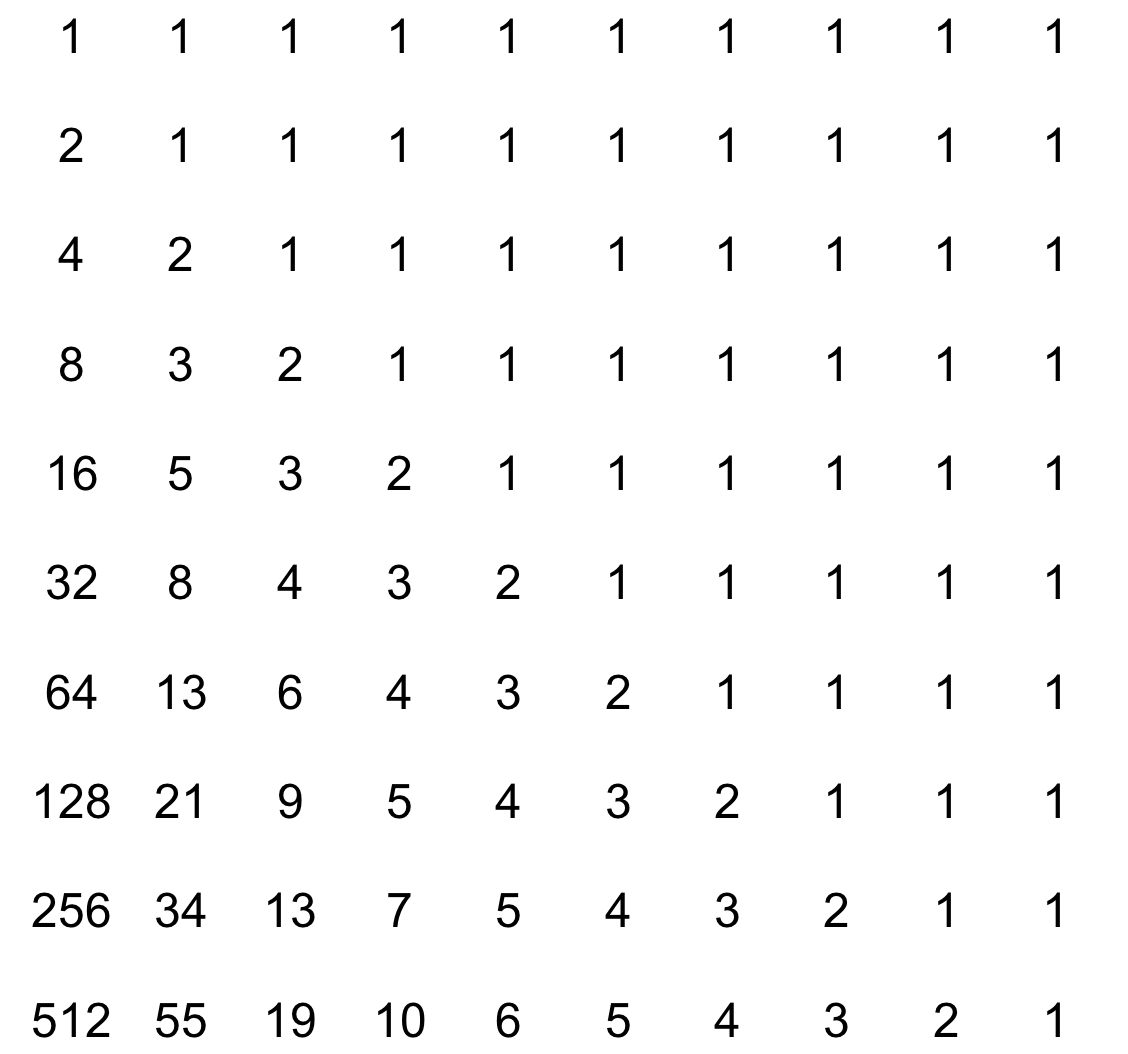
Abb. 1: Matrix
Die Matrix ist eine Folge von Folgen.
3 Rückgriffe
Die Zahlen 1, 1, 1, 2, 3, 4, 6, 9, 13, 19 der dritten Spalte sind gemäß Abbildung 2 konstruiert.
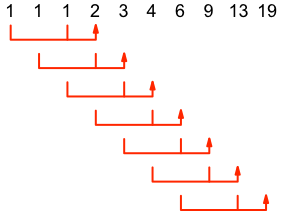
Abb. 2: Konstruktion der Zahlen der dritten Spalte
Wir haben drei Startwerte, alle 1. Die weiteren Zahlen sind jeweils die Summe der unmittelbar vorangegangenen Zahl und der zwei Schritte weiter zurückliegenden Zahl.
Dies gilt entsprechend allgemein: Die Zahlen a[i,k] in der k-ten Spalte haben zunächst k Startwerte 1, also a[i,k] = 1 für i = 1 .. k. Die nachfolgenden Zahlen genügen der Rekursion:
a[i,k] = a[i-1,k] + a[i-k,k]
Für k = 1 ergibt
sich die Verdoppelungsfolge, für k = 2 die übliche Fibonacci-Folge.
4 Determinanten
Es ist:
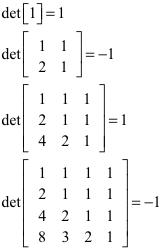
Die Determinanten sind alternierend ±1. Ohne Beweis
5 Grenzwerte
In der Tabelle 1 sind für die ersten fünf Spalten die Quotienten aufeinanderfolgender Folgenglieder eingetragen. Bei der Verdoppelungsfolge ist dieser Quotient konstant 2. Bei der Fibonacci-Folge erscheint der Goldene Schnitt als Grenzwert.
|
n |
a[n+1,1]/a[n,1] |
a[n+1,2]/a[n,2] |
a[n+1,3]/a[n,3] |
a[n+1,4]/a[n,4] |
a[n+1,5]/a[n,5] |
|
1 |
2. |
1. |
1. |
1. |
1. |
|
2 |
2. |
2. |
1. |
1. |
1. |
|
3 |
2. |
1.500000000 |
2. |
1. |
1. |
|
4 |
2. |
1.666666667 |
1.500000000 |
2. |
1. |
|
5 |
2. |
1.600000000 |
1.333333333 |
1.500000000 |
2. |
|
6 |
2. |
1.625000000 |
1.500000000 |
1.333333333 |
1.500000000 |
|
7 |
2. |
1.615384615 |
1.500000000 |
1.250000000 |
1.333333333 |
|
8 |
2. |
1.619047619 |
1.444444444 |
1.400000000 |
1.250000000 |
|
9 |
2. |
1.617647059 |
1.461538462 |
1.428571429 |
1.200000000 |
|
10 |
2. |
1.618181818 |
1.473684211 |
1.400000000 |
1.333333333 |
|
11 |
2. |
1.617977528 |
1.464285714 |
1.357142857 |
1.375000000 |
|
12 |
2. |
1.618055556 |
1.463414634 |
1.368421053 |
1.363636364 |
|
13 |
2. |
1.618025751 |
1.466666667 |
1.384615385 |
1.333333333 |
|
14 |
2. |
1.618037135 |
1.465909091 |
1.388888889 |
1.300000000 |
|
15 |
2. |
1.618032787 |
1.465116279 |
1.380000000 |
1.307692308 |
|
16 |
2. |
1.618034448 |
1.465608466 |
1.376811594 |
1.323529412 |
|
17 |
2. |
1.618033813 |
1.465703971 |
1.378947368 |
1.333333333 |
|
18 |
2. |
1.618034056 |
1.465517241 |
1.381679389 |
1.333333333 |
|
19 |
2. |
1.618033963 |
1.465546218 |
1.381215470 |
1.325000000 |
|
20 |
2. |
1.618033999 |
1.465596330 |
1.380000000 |
1.320754717 |
|
|
|
|
|
|
|
|
lim |
2 |
1.618033989 |
1.465571232 |
1.380277569 |
1.324717957 |
Tab. 1: Quotienten-Folgen und Grenzwerte
Für die Spalte k erhalten wir den Grenzwert als positive Lösung der Gleichung:
![]()
Das sind auch die positiven Nullstellen (Abb. 3) der Funktionen:
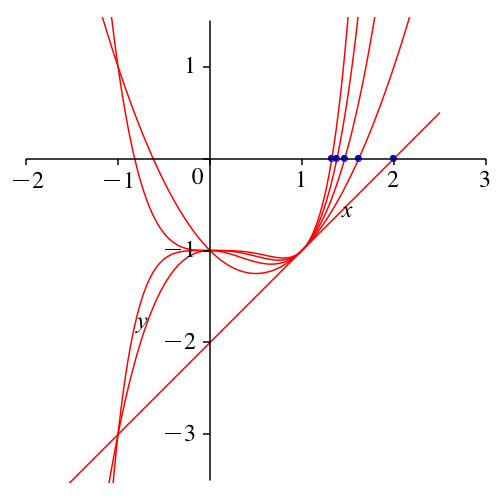
Abb. 3: Grenzwerte als Nullstellen
Weblinks
Hans Walser: Halbstreifen
http://www.walser-h-m.ch/hans/Miniaturen/H/Halbstreifen/Halbstreifen.html