Hans Walser, [20150835]

Fibonacci-Mauern

Anregung: R. H., L.

1        Die Klassische Fibonacci-Mauer

Die Fibonacci-Folge hat die Startwerte  und  und die Rekursion:

 

                                                                                                             (1)

 

Explizit in Zahlen:

 

              0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ...         (2)

 

Wir bauen eine Zahlenmauer mit den Fibonacci-Zahlen in der Basis (Abb. 1).

 

                          2584

                        987  1597

                     377   610   987

                  144   233   377   610

                55    89   144   233   377

             21    34    55    89   144   233

           8    13    21    34    55    89   144

        3     5     8    13    21    34    55    89

     1     2     3     5     8    13    21    34    55

  0     1     1     2     3     5     8    13    21    34

 

Abb. 1: Fibonacci-Mauer

 

Wir erkennen allerhand, zum Beispiel:

In den SchrŠgen parallel zum Dach rechts haben wir Ausschnitte aus der Fibonacci-Folge.

In den SchrŠgen parallel zum Dach links haben wir Ausschnitte aus der Folge die entsteht wenn wir von der Fibonacci-Folge nur jedes zweite Glied nehmen (SchrittlŠnge 2). Die Folge hat bei Nummerierung von unten nach oben die Rekursion:

 

                                                                                                         (3)

 

Die senkrechten Spalten sind bei Nummerierung von unten nach oben Ausschnitte aus der Fibonacci-Folge mit SchrittlŠnge 3. Es gilt die Rekursion:

 

                                                                                                       (4)

 

†ber Fibonacci-Teilfolgen der SchrittlŠnge k siehe (Walser 2012, S. 55-57).

2     Negative Indizes

Wir setzen die Fibonacci-Folge nach links das hei§t fŸr negative Indizes kompatibel mit (1) fort (Tab. 1):

 

n

–6

–5

–4

–3

–2

–1

0

1

2

3

4

5

6

–8

5

–3

2

–1

1

0

1

1

2

3

5

8

Tab. 1: Negative Indizes

 

Die Fibonacci-Zahlen mit negativen Indizes haben alternierende Vorzeichen.

Es ist:

 

                                                                                                              (5)

 

3     ãNegativeÒ Fibonacci-Mauer

Wir bauen eine Fibonacci-Mauer mit Fibonacci-Zahlen mit negativen Indizes in der Basis (Abb. 2). In der Basis haben die negativen Zahlen ein stŠrkeres Geweicht als die positiven Zahlen. Die Basissumme ist –12.

 

                             21

                           8    13

                        3     5     8

                     1     2     3     5

                  0     1     1     2     3

              -1     1     0     1     1     2

           -3     2    -1     1     0     1     1

        -8     5    -3     2    -1     1     0     1

    -21    13    -8     5    -3     2    -1     1     0

 

Abb. 2: ãNegativeÒ Fibonacci-Mauer

 

Wir sehen, dass wir bereits auf halber Hšhe aus den negativen Zahlen heraus sind. Das Element an der Spitze ist das grš§te Element in der ganzen Mauer und das Negative vom kleinsten Element.

In den SchrŠgen parallel zum Dach rechts haben wir Ausschnitte aus der (erweiterten) Fibonacci-Folge.

In den SchrŠgen parallel zum Dach links haben die Rekursion (2).

4     Hoch- und Tiefbau

Die Abbildung 3 zeigt einen reduzierten Ausschnitt der Fibonacci-Mauer der Abbildung 1 in schwarz. In rot wurde ein passender Unterbau zugefŸgt.

 

                          55   

                       21    34   

                     8    13    21   

                  3     5     8    13   

               1     2     3     5     8   

            0     1     1     2     3     5    

        -1     1     0     1     1     2     3

     -3     2    -1     1     0     1     1     2

  -8     5    -3     2    -1     1     0     1     1

 

Abb. 3: Unterbau

 

Wir sehen, dass sich die Fibonacci-Folge mit negativen Indizes entwickelt.

Das ist allerdings nicht die einzige Lšsung. Die Abbildung 4 zeigt eine weitere Lšsung. Dabei wurde willkŸrlich jeweils mit 7 begonnen. Die Rekursion (1) gilt nicht mehr.

 

                          55   

                       21    34   

                     8    13    21   

                  3     5     8    13   

               1     2     3     5     8    

            0     1     1     2     3     5    

         7    -7     8    -7     9    -6    11

      7     0    -7    15   -22    31   -37    48

   7     0     0    -7    22   -44    75  -112   160

 

Abb. 4: Weitere Lšsung

 

Es ist klar, dass es unendlich viele Lšsungen gibt. Wir kšnnen jede Unterbauzeile mit einer beliebigen Zahl starten.

5     Modulo

5.1    Farbcode

Wir fŠrben die Bausteine modulo k ein.

Die Abbildung 5.1 gibt den verwendeten Farbcode.

 

Abb. 5.1: Farbcode

 

Die Basis lassen wir in den folgenden Beispielen von  bis  laufen. Das hat den Vorteil, dass 12 und 144 recht viele Teiler haben. Wenn die Modulzahl ein Teiler von 12 ist, haben wir schwarz in allen Ecken.

5.2    Modulo 2

Wir unterscheiden zwischen gerade (schwarz, 0) und ungerade (blau, 1).

 

Abb. 5.2: Modulo 2

 

5.3    Modulo 3

Abb. 5.3: Modulo 3

 

5.4    Modulo 4

Abb. 5.4: Modulo 4

 

5.5    Modulo 5

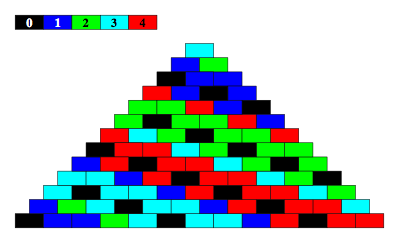
Abb. 5.5: Modulo 5

 

5.6    Modulo 6

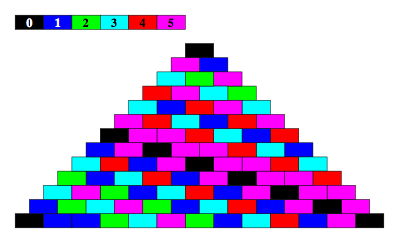
Abb. 5.6: Modulo 6

 

5.7    Modulo 7

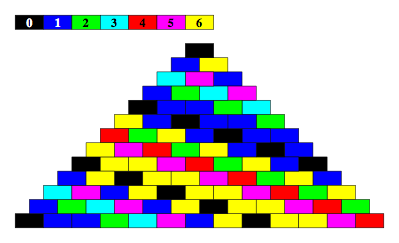
Abb. 5.7: Modulo 7

 

5.8    Modulo 8

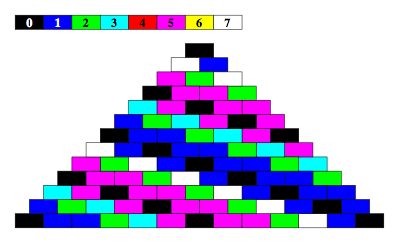
Abb. 5.8: Modulo 8

 

5.9    Modulo 9

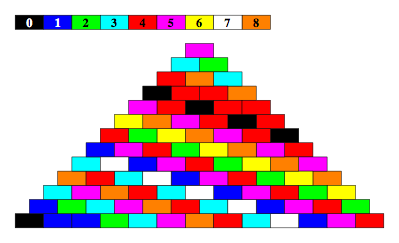
Abb. 5.9: Modulo 9

 

5.10 Modulo 10

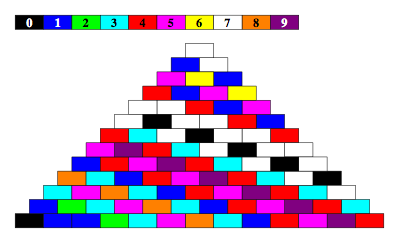
Abb. 5.10: Modulo 10

 

5.11 Modulo 11

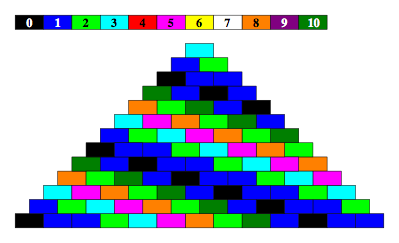
Abb. 5.11: Modulo 11

 

5.12 Modulo 12

Abb. 5.12: Modulo 12

 

6     Fehlende Farben

In einigen Abbildungen 5.2 bis 5.11 fehlen einzelne Farben.

6.1    Modulo  8

Es fŠllt auf, dass in der Abbildung 5.8 die rote Farbe fehlt.

6.1.1   Vermutung

Es gibt kein  mit .

Mit brute force fŸr n = 0, ... , 100'000 verifiziert.

6.1.2   Beweis

Die Folge  kann nur Werte aus  annehmen. Daher kšnnen Paare aufeinanderfolgender Folgenglieder  nur Werte aus  annehmen. Das sind 64 mšgliche Wertepaare. Nach dem Schubfachprinzip von Dirichlet (pigeonhole principle) muss sich das Start-Wertepaar  nach spŠtestens 64 Schritten wiederholen. Dann fŠngt die Periode an. Wir brauchen also nur die ersten 64 Folgenglieder von  durchzukŠmmen.

TatsŠchlich wiederholt sich das Wertepaar  schon eher (Tab. 2). Die PeriodenlŠnge ist 11. In der Periode erscheint die Zahl 4 nicht.

 

n

0

1

2

3

4

5

6

7

8

9

10

11

12

13

0

1

1

2

3

5

0

5

5

2

7

1

0

1

Tab. 2: Modulo 8

 

6.2    Modulo 11

In der Abbildung 5.11 fehlen die Farben Rot, Wei§ und Lila.

Vermutung:

Beweis analog 6.1.2. Wir haben die ersten 121 Werte zu untersuchen. Die Periode beginnt schon frŸher (Tab. 3).

 

n

0

1

2

3

4

5

6

7

8

9

10

11

0

1

1

2

3

5

8

2

10

1

0

1

Tab. 3: Modulo 11

 

In der Periode erscheint keine der Zahlen 4, 7, 9.

†ber Fibonacci-Zahlen modulo k siehe (Walser 2012, S. 71-75).

Literatur

Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.