Hans Walser, [20150819]

Fibonacci-Potenzen

1     Fibonacci-Quadrate

Das Wachstum der Fibonacci-Folge lŠsst sich sehr schšn mit der oft gesehenen Abbildung 1 illustrieren. Beim Start mit einem Einheitsquadrat sind die SeitenlŠngen der Quadrate sind gerade die Fibonacci-Zahlen.

 

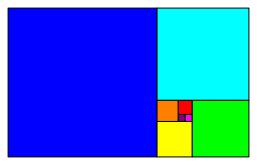
Abb. 1: Fibonacci-Quadrate

 

FŸr die SeitenlŠngen ergibt sich also:

 

                                                     1, 1, 2, 3, 5, 8, 13, 21, ...                                                (1)

 

FŸr diese Folge gilt die Rekursion:

 

                                                                                                             (2)

 

2     Fibonacci-Quadrat-FlŠchen

FŸr die FlŠcheninhalte der Quadrate der Abbildung 1 finden wir:

 

                                                 1, 1, 4, 9, 25, 64, 169, 441, ...                                            (3)

 

Mit einigem TŸfteln finden wir die dreistellige Rekursion:

 

                                                                                             (4)

 

Beweis durch Nachrechnen unter BenŸtzung von (2).

Beispiel (n = 8):

 

                                                    

 

Das kann auch in der Form

 

                                                  

 

geschrieben werden. Geometrisch hei§t das (Abb. 2), dass das ganz gro§e und das ganz kleine Quadrat zusammen flŠchenmŠ§ig gleich dem Doppelten der beiden mittleren Quadrate sind.

 

       

Abb. 2: Blau plus gelb = zwei mal (grŸn plus cyan)

 

Dies kann durch den Zerlegungsbeweis der Abbildung 3 unmittelbar eingesehen werden.

 

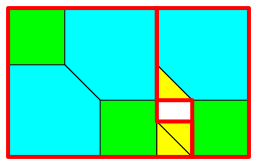
Abb. 3: Zerlegung

 

Bei dreistelligen Rekursionen spricht man manchmal von einer ãTribonacci-FolgeÒ. (Sprachlich korrekt mŸsste dann allerdings die gewšhnliche Fibonacci-Folge als ãBibonacci-FolgeÒ bezeichnet werden.)

Damit ist das Thema umrissen: Welche Rekursionen gelten fŸr die k-ten Potenzen der Fibonacci-Zahlen.

3     Bezeichnungen

Wir werden sehen, dass wir fŸr die k-te Potenz eine (k + 1)-stellige Rekursion erhalten.

FŸr die k-te Potenz machen wir daher den Ansatz:

 

                                         (5)

 

4     Resultate. Zahlendreieck

Mit einigem Rechnen erhalten wir:

 

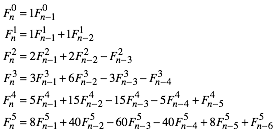                                                            (7)

 

 

 

 

 

 

 

Die Abbildung 4 zeigt das zugehšrige Zahlendreieck. 

 

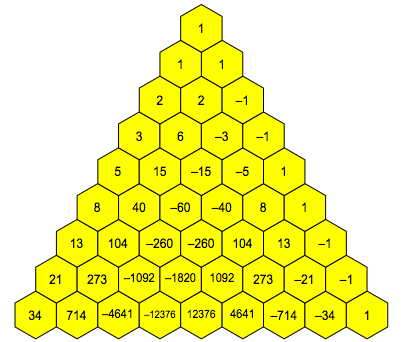
Abb. 4: Zahlendreieck

 

Das Zahlendreieck hat in Zweierschritten alternierende Vorzeichen.

Abgesehen von den Vorzeichen ist es beinahe symmetrisch. Wir kšnnen (abgesehen von den Vorzeichen) eine Symmetrie erreichen, wenn wir die Rekursionen (7) in der ãNull-FormÒ schreiben:

 

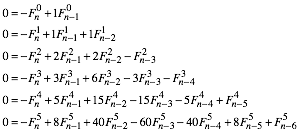                                     (8)

 

 

 

 

 

 

 

In der ersten SchrŠgzeile der Abbildung 2 erscheinen die Fibonacci-Zahlen.

In der zweiten SchrŠgzeile sitzen die Produkte zweier aufeinanderfolgender Fibonacci-Zahlen. Diese genŸgen interessanterweise derselben Rekursion wie die Quadrate der Fibonacci-Zahlen.

In der dritten SchrŠgzeile sitzen Zahlen, welch der Rekursion der Kuben der Fibonacci-Zahlen genŸgen.

Und so weiter.

Das Zahlendreieck ist also der SchlŸssel zu sich selber.

5     Rechnerisches und Technisches

FŸr die Herleitung wurde die Formel von Binet verwendet (Walser 2012, S. 13, und Walser 2013, S. 106): Mit

 

                                                 (Goldener Schnitt)                                           (9)

 

ist:

 

                                                                                                 (10)

 

Man sieht dann auch, dass man tatsŠchlich mit einer (k + 1)-stelligen Rekursion durchkommt. FŸr die Rechnungen wurde CAS verwendet.

 

Literatur

Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.