Hans Walser, [20210813]

Fibonacci-Rekursion

1 Worum geht es?

Iteration der Fibonacci-Rekursion:

(1)

Mit den Startwerten 1 und 1 ergeben sich die Fibonacci-Zahlen (Abb. 1).

Abb. 1: Fibonacci-Zahlen

Bei der Rekursionsformel (1) müssen zur Berechnung einer Fibonacci-Zahl die beiden unmittelbar vorangehenden Fibonacci-Zahlen bekannt sein.

2 Iterationen

Durch Anwendung von (1) auf sich selber erhalten wir:

(2)

Wir führen das Verfahren weiter:

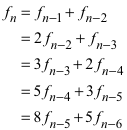(3)

Als Koeffizienten ergeben sich wiederum die Fibonacci-Zahlen:

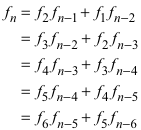(4)

Beweis induktiv.

3 Allgemein

Für die Rekursion mit der Tiefe k gilt:

(5)

4 Sonderfälle

Wir versuchen, mit möglichst kleinen Fibonacci-Zahlen auszukommen. Dazu eine Fallunterscheidung.

4.1 Ungerader Index

Es sei n = 2m + 1. Für k = m erhalten wir aus (5):

(6)

Die Abbildung 2 illustriert die Formel (6) exemplarisch für n = 11.

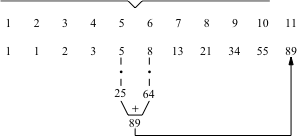
Abb. 2: Ungerader Index

4.2 Gerader Index

Es sei n = 2m. Für k = m erhalten wir aus (5):

(7)

Die Abbildung 3 illustriert die Formel (7) exemplarisch für n = 12.

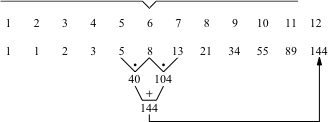
Abb. 3: Gerader Index

4.3 Superformel

Die Formeln (6) und (7) können zusammengefasst werden:

(8)

Hier kann man das Hohe Lied über die Schönheit der Mathematik singen.

Dabei bedeuten und das Auf- beziehungsweise Abrunden von x auf die nächste ganze Zahl. Dafür werden auch die Bezeichnungen ceil(x) beziehungsweise floor(x) verwendet.

Mit den beiden Startwerten 1 und 1 können mit (8) sämtliche Fibonacci-Zahlen berechnet werden.

5 Weitere Beispiele

Die Abbildungen 4 zeigen alle Möglichkeiten für n = 11. Die Veränderungen der Teilsummen folgen ebenfalls dem Fibonacci-Rhythmus.

Abb. 4.1

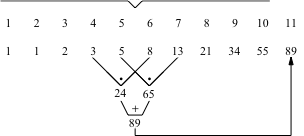
Abb. 4.2

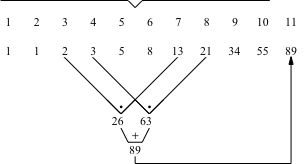
Abb. 4.3

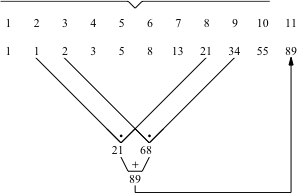
Abb. 4.4

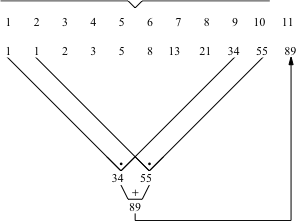
Abb. 4.5: Übliche Rekursion

Die Abbildungen 5 zeigen alle Möglichkeiten für n = 12.

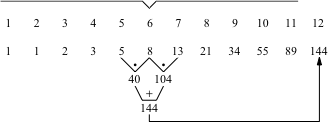
Abb. 5.1

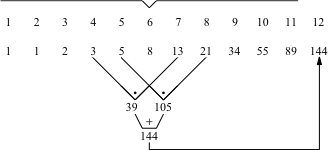
Abb. 5.2

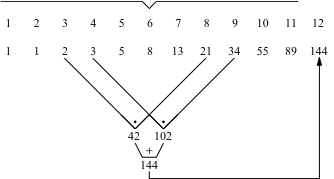
Abb. 5.3

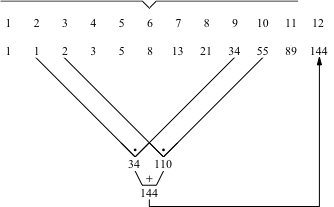
Abb. 5.4

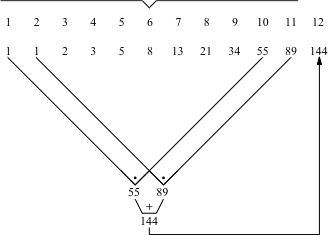
Abb. 5.5: Ein alter Bekannter

Websites

Hans Walser: Binomialkoeffizienten

http://www.walser-h-m.ch/hans/Miniaturen/B/Binomialkoeff2/Binomialkoeff2.html