Hans Walser, [20240427]

Fibonacci-Spiralen

1 Worum es geht

Beispiele von Spiralen aus regelmäßigen Dreiecken und Sechsecken, deren Seitenlängen die Fibonacci-Zahlen 1, 1, 2, 3, 5, 8, 13, ... sind.

Die Idee dabei ist, dass die Spiralen beidseitig eingepackt sind.

2 Der Klassiker

Der Klassiker besteht nur aus regelmäßigen Dreiecken (Abb. 1). Es sind zwei ineinandergewickelte Spiralen, eine Doppelspirale also. In der Abbildung 1 haben die Dreiecke die Seitenlängen 1, 1, 2, 3, 5, 8.

Abb. 1: Der Klassiker

Die Abbildung 2 zeigt eine weitere Runde. Die Seitenlängen der Dreiecke sind 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. Die orange Spirale ist innen und außen von der hellblauen Spirale eingepackt, und umgekehrt.

Abb. 2: Zweite Runde

Abb. 3: Die ersten beiden Runden

3 Spiralen mit Dreiecken und Sechsecken

Im Folgenden einige Beispiele.

3.1 Einfache Spiralen

3.1.1 Beispiel 1

Abb. 4.1: Erste Runde

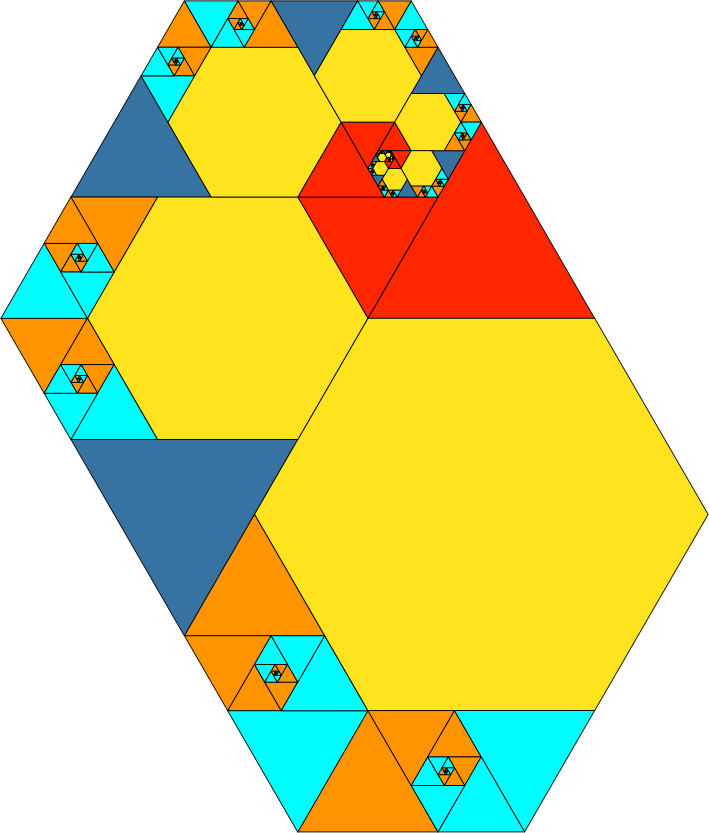
Abb. 4.2: Die ersten beiden Runden

3.1.2 Beispiel 2

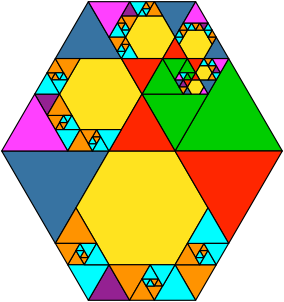
Abb. 5.1

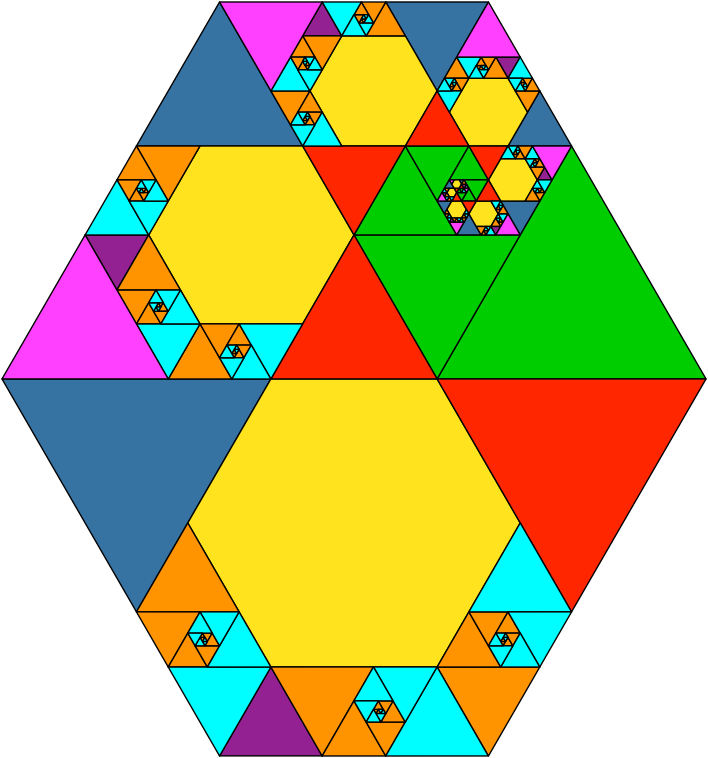
Abb. 5.2

3.1.3 Beispiel 3

Abb. 6.1

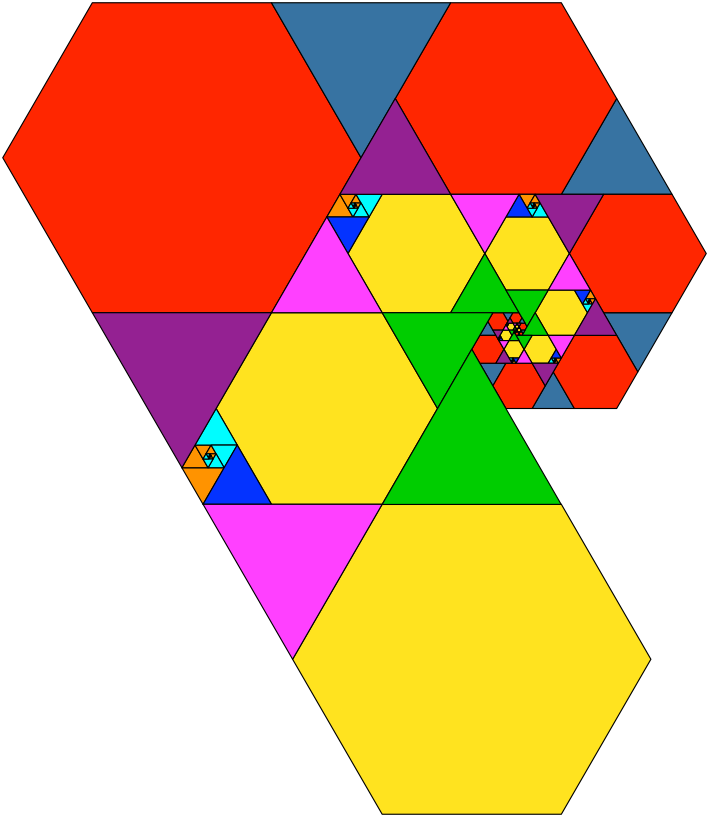
Abb. 6.2

3.2 Doppelspiralen

3.2.1 Beispiel 1

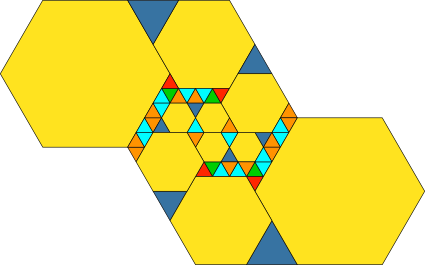
Abb. 7

3.2.2 Beispiel 2

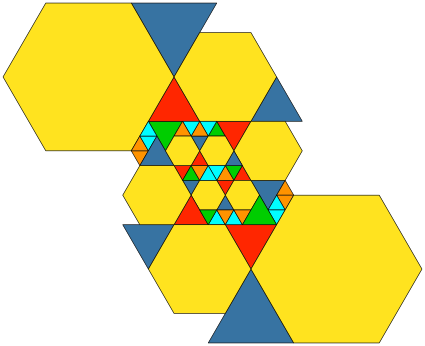
Abb. 8

3.2.3 Beispiel 3

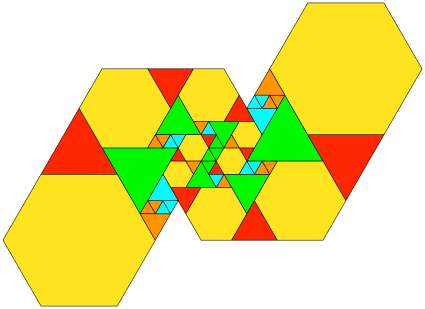
Weblinks

Hans Walser: Miniaturen: Fibonacci

https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Fibonacci/index.html

Hans Walser: Miniaturen: Spiralen und Schraubenlinien

https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Spiralen/index.html

Literatur

Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.

Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).