Hans Walser, [20090625c]
Fibonacci-Trapeze
Anregung: [Deshpande
2009]
1 Hexagon mit angesetzten Quadraten
1.1
Basisfigur
Wir basieren unsere
Überlegungen auf folgender Figur. Einem zentralen Hexagon werden Quadrate
angesetzt.
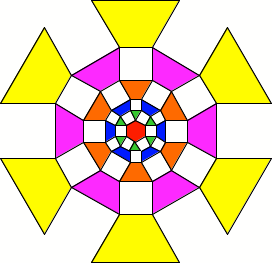
Hexagon mit aufgesetzten
Quadraten
Die Trapeze sind
offensichtlich gleichschenklig und haben die Basiswinkel 60°. Sind sie auch
ähnlich?
1.2
Analyse der Trapeze
Wir interpretieren das
grüne Dreieck mit etwas Gewalt als Trapez. Es hat die Unterkante 1, die
Schenkel 1 und die Oberkante 0.
Bei den Trapezen
bezeichnen wir die längere Parallelseite als Unterkante, die kürzere als Oberkante.
Wir können die Trapeze maßgetreu in einen Dreiecksraster einzeichnen.

Trapeze im
Dreiecksraster
Die Trapeze sind
offensichtlich nicht ähnlich.
Es gilt:
|
Ring Nr. |
Farbe |
Oberkante |
Schenkel |
Unterkante |
|
0 |
grün |
0 |
1 |
1 |
|
1 |
blau |
1 |
1 |
2 |
|
2 |
orange |
1 |
2 |
3 |
|
3 |
magenta |
2 |
3 |
5 |
|
4 |
gelb |
3 |
5 |
8 |
Das riecht nach
Fibonacci.
Die Trapeze im Ring Nr.
n haben die Oberkante ![]() , die Schenkel
, die Schenkel ![]() und
die Unterkante
und
die Unterkante ![]() .
.
1.3
Induktionsbeweis
Aussage für ![]() (blaue Trapeze)
richtig.
(blaue Trapeze)
richtig.
Aussage sei richtig bis
und mit Ring Nr. n (Beweisfigur, äußerer
hellgrüner Ring).
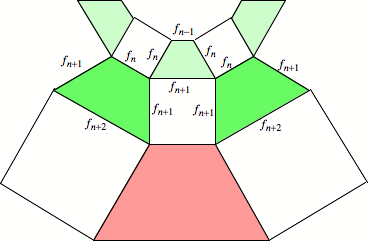
Beweisfigur
Ein Trapez im Ring Nr. ![]() hat dann die
Oberkante
hat dann die
Oberkante ![]() (Quadrat der
Seitenlänge
(Quadrat der
Seitenlänge ![]() ) und die Schenkel
) und die Schenkel ![]() (Quadrate der
Seitenlänge
(Quadrate der
Seitenlänge ![]() ). Für die Unterkante zerlegen wir gemäß Figur in ein
Parallelogramm und ein Dreieck.
). Für die Unterkante zerlegen wir gemäß Figur in ein
Parallelogramm und ein Dreieck.
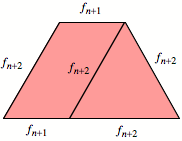
Zerlegung
Die Unterkante hat also
die Länge ![]() .
.
1.4
Goldenes Trapez
Wenn wir die
Konstruktion nach außen weiterführen, nehmen die Trapeze immer mehr die Form an
eines Trapezes mit der Oberkante ![]() , der Schenkel 1 und der Unterkante
, der Schenkel 1 und der Unterkante ![]() . Dabei ist
. Dabei ist ![]() und
und ![]() (goldener
Schnitt). Dieses Trapez nennen wir daher das goldene Trapez. Die Basiswinkel des goldenen Trapezes sind 60°.
(goldener
Schnitt). Dieses Trapez nennen wir daher das goldene Trapez. Die Basiswinkel des goldenen Trapezes sind 60°.
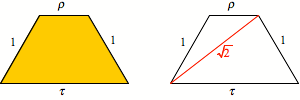
Goldenes Trapez
Das goldene Trapez hat
eine bemerkenswerte Eigenschaft: Seine Diagonale hat exakt die Länge ![]() . Das kann mit dem Kosinussatz nachgewiesen werden.
. Das kann mit dem Kosinussatz nachgewiesen werden.
Wir können also sechs
goldene Trapeze im Wechsel mit sechs Einheitsquadraten zu einem Ring zusammenfügen,
wobei alle Diagonalen gleich lang sind.
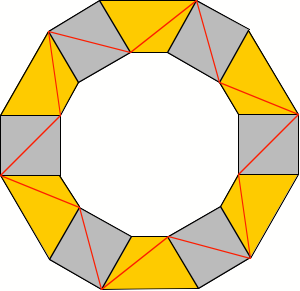
Ring mit gleich langen
Diagonalen
In den
Fibonacci-Trapezen ist die Diagonale natürlich nur näherungsweise das ![]() der
Schenkellänge. Im Trapez
der
Schenkellänge. Im Trapez ![]() hat die
Diagonale
hat die
Diagonale ![]() die Länge:
die Länge:
![]()
Somit ist:
![]()
Direkter Beweis:
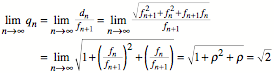
Tabelle:
q[1] = 1.322875656
q[2] =
1.452966315
q[3] = 1.4
q[4] =
1.419727086
q[5] =
1.412119981
q[6] =
1.415015044
q[7] =
1.413907687
q[8] =
1.414330435
q[9] =
1.414168927
q[10] = 1.414230612
q[11] = 1.41420705
q[12] = 1.41421605
q[13] = 1.414212612
q[14] = 1.414213925
q[15] = 1.414213424
q[16] = 1.414213615
q[17] = 1.414213542
q[18] = 1.41421357
q[19] = 1.414213559
q[20] = 1.414213564
q[21] = 1.414213562
q[22] = 1.414213563
q[23] = 1.414213562
q[24] = 1.414213562
Bemerkenswert ist das
schöne rationale Zwischenresultat ![]() .
.
1.5
Eine Spirale
Wir können die Trapeze
im Dreiecksraster zu einer Spirale zusammenfügen.
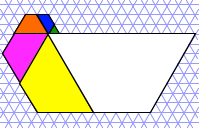
Spirale aus
Fibonacci-Trapezen
Die Eckpunkte liegen im
Grenzfall auf einer logarithmischen Spirale. Rechts sind die Trapeze von 0 bis
29 gezeichnet.
1.6
Flächeninhalt
Das Trapez ![]() im ring Nr. n hat den Flächeninhalt:
im ring Nr. n hat den Flächeninhalt:
![]()
Insbesondere hat das
grüne Dreieck, also ![]() , den Flächeninhalt
, den Flächeninhalt ![]() . Wir nehmen diesen Flächeninhalt als Vergleichsmaß und erhalten
so für das Trapez
. Wir nehmen diesen Flächeninhalt als Vergleichsmaß und erhalten
so für das Trapez ![]() den relativen
Flächeninhalt:
den relativen
Flächeninhalt:
![]()
Tabellarisch sieht das
so aus:
psi(t[0]) = 1
psi(t[1]) = 3
psi(t[2]) = 8
psi(t[3]) = 21
psi(t[4]) = 55
psi(t[5]) = 144
psi(t[6]) = 377
psi(t[7]) = 987
psi(t[8]) = 2584
psi(t[9]) = 6765
psi(t[10])
= 17711
Zum Vergleich:
f[2*(0+1)] = 1
f[2*(1+1)] = 3
f[2*(2+1)] = 8
f[2*(3+1)] = 21
f[2*(4+1)] = 55
f[2*(5+1)] = 144
f[2*(6+1)] = 377
f[2*(7+1)] = 987
f[2*(8+1)] = 2584
f[2*(9+1)] = 6765
f[2*(10+1)]
= 17711
Offenbar gilt die
Identität:
![]()
Der Beweis geht über
die Formel von Binet.
2
Andere Vielecke im Zentrum
2.1
Dreieck im Zentrum
2.1.1
Reguläres Dreieck im Zentrum
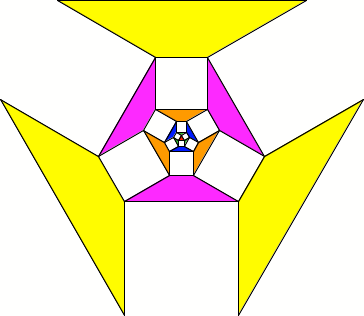
Reguläres Dreieck im
Zentrum
Die gleichschenkligen
Trapeze haben nun Basiswinkel 30°. Es gilt:
|
Ring Nr. |
Farbe |
Oberkante |
Schenkel |
Unterkante |
Relative Fläche |
|
0 |
grün |
0 |
1 |
|
1 (Einheit) |
|
1 |
blau |
1 |
|
4 |
5 |
|
2 |
orange |
|
4 |
|
24 |
|
3 |
magenta |
4 |
|
19 |
115 |
|
4 |
gelb |
|
19 |
|
551 |
Es gilt die Rekursion:
![]()
Weiter ist:
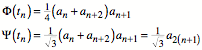
Es gilt die Rekursion:
![]()
Die Spirale wächst
happig:
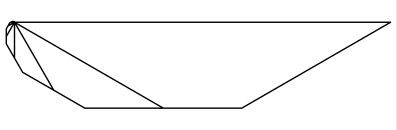
Spirale
2.1.2
Beliebiges Dreieck im Zentrum
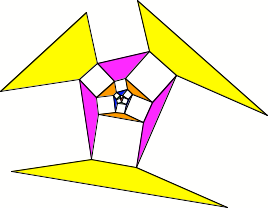
Beliebiges Dreieck im
Zentrum
Wir haben immer noch
Trapeze, aber keine gleichschenkligen mehr. Das Experiment (Cabri) zeigt, dass
die Flächenrelationen noch stimmen:
|
Ring Nr. n |
Farbe |
Relative Fläche |
|
0 |
grün |
1 (Einheit) |
|
1 |
blau |
5 |
|
2 |
orange |
24 |
|
3 |
magenta |
115 |
|
4 |
gelb |
551 |
Für den Fall ![]() gibt [Deshpande
2009] einen proof without words. Für den allgemeinen Fall habe ich keinen
Beweis.
gibt [Deshpande
2009] einen proof without words. Für den allgemeinen Fall habe ich keinen
Beweis.
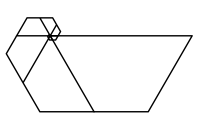
Spiralen gibt es auch hier, sogar drei Stück. Wir wählen aus der Figur eine geeignete Folge von Trapezen aus (geht auf drei Arten), die wir dann „einrollen“.
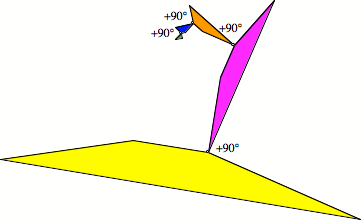
Auswahl von Trapezen

Spirale
2.2
Viereck im Zentrum
2.2.1
Quadrat im Zentrum
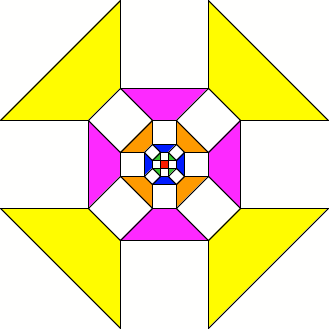
Quadrat im Zentrum
Die gleichschenkligen
Trapeze haben nun Basiswinkel 45°. Es gilt:
|
Ring Nr. |
Farbe |
Oberkante |
Schenkel |
Unterkante |
Relative Fläche |
|
0 |
grün |
0 |
1 |
|
1 (Einheit) |
|
1 |
blau |
1 |
|
3 |
4 |
|
2 |
orange |
|
3 |
|
15 |
|
3 |
magenta |
3 |
|
11 |
56 |
|
4 |
gelb |
|
11 |
|
209 |
Es gilt die Rekursion:
![]()
Weiter ist:
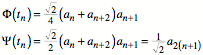
Es gilt die Rekursion:
![]()
Die Spirale wächst:
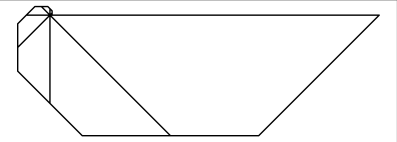
Spirale
2.2.2
Parallelogramm im Zentrum
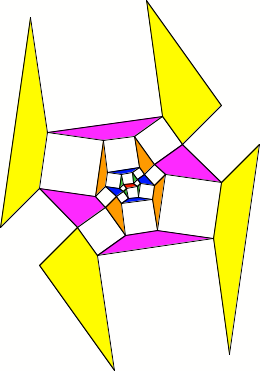
Parallelogramm im
Zentrum
Mit einem
Parallelogramm geht es aber.
|
Ring Nr. |
Farbe |
Relative Fläche |
|
0 |
grün |
1 (Einheit) |
|
1 |
blau |
4 |
|
2 |
orange |
15 |
|
3 |
magenta |
56 |
|
4 |
gelb |
209 |
Beweis?
Mit einem allgemeinen
Viereck im Zentrum geht es nicht; die Trapeze in einem Ring sind nicht mehr
flächengleich. Das Dreieck ist ein Sonderfall.
Vermutlich funktioniert
es allgemein für affinreguläre Vielecke.
Literatur
[Deshpande 2009] Deshpande,
M. N. : Proof Without Words: Beyond Extriangles. MATHEMATICS MAGAZINE. Vol. 82,
No. 3, June 2009, p. 208.