Hans Walser, [20100314a]
Fibonacci 2d
Anregung: A. W., L.
1 Idee
Die Fibonacci-Zahlen werden modulo m berechnet. Dadurch entsteht eine periodische Folge. Nun wird die Multiplikationstabelle oder die Additionstabelle, ebenfalls modulo m, berechnet. Es entsteht eine doppelt periodische Tabelle. Die EintrŠge in der Multiplikationstabelle werden farblich codiert.
2 Quersumme
Die
Quersumme einer Zahl ist dasselbe wie die Zahl mod 9, wobei 0 mod 9 durch 9
codiert wird. Dadurch erhalten wir Zahlen aus 
statt 
.
Die Folge der Quersummen der Fibonacci-Zahlen beginnt so:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9, 1, 1, ...
Nach 24 Schritten wiederholen sich die Startwerte, und die Periode beginnt. Nach 12 Schritten haben wir eine Antiperiode, indem die Summe der Zahlen der zweiten Zwšlfer-Gruppe mit den entsprechenden Zahlen der ersten Zwšlfer-Gruppe jeweils 9 ist.
2.1 Multiplikation
Multiplikationstabelle
----------------------
* | 112358437189887641562819
----------------------------
1 | 112358437189887641562819
1 | 112358437189887641562819
2 | 224617865279775382134729
3 | 336966393369663933696639
5 | 551674268549448325731459
8 | 887641562819112358437189
4 | 448325731459551674268549
3 | 336966393369663933696639
7 | 775382134729224617865279
1 | 112358437189887641562819
8 | 887641562819112358437189
9 | 999999999999999999999999
8 | 887641562819112358437189
8 | 887641562819112358437189
7 | 775382134729224617865279
6 | 663933696639336966393369
4 | 448325731459551674268549
1 | 112358437189887641562819
5 | 551674268549448325731459
6 | 663933696639336966393369
2 | 224617865279775382134729
8 | 887641562819112358437189
1 | 112358437189887641562819
9 | 999999999999999999999999
Farblich codiert:
Multiplikation farblich codiert
Wegen der Antiperiode haben wir rechts unten dasselbe Muster wie links oben.
Im folgenden Bild sind die 48 ersten Zahlen aufgenommen. Das Muster wiederholt sich.
Zwei PeriodenlŠngen
2.2 Addition
Additionstabelle
----------------
+ | 112358437189887641562819
----------------------------
1 | 223469548291998752673921
1 | 223469548291998752673921
2 | 334571659312119863784132
3 | 445682761423221974895243
5 | 667814983645443296127465
8 | 991247326978776539451798
4 | 556793872534332185916354
3 | 445682761423221974895243
7 | 889136215867665428349687
1 | 223469548291998752673921
8 | 991247326978776539451798
9 | 112358437189887641562819
8 | 991247326978776539451798
8 | 991247326978776539451798
7 | 889136215867665428349687
6 | 778925194756554317238576
4 | 556793872534332185916354
1 | 223469548291998752673921
5 | 667814983645443296127465
6 | 778925194756554317238576
2 | 334571659312119863784132
8 | 991247326978776539451798
1 | 223469548291998752673921
9 | 112358437189887641562819
Farblich codiert:
Addition farblich codiert
Im folgenden Bild sind die 48 ersten Zahlen aufgenommen. Das Muster wiederholt sich.
Zwei PeriodenlŠngen
3 Letzte Ziffer
Statt der Quersumme kšnnen wir einfach die letzte Ziffer in der Dezimaldarstellung der Fibonacci-Zahlen nehmen. Dies bedeutet, dass wir modulo 10 rechnen. Die PeriodenlŠnge ist 60.
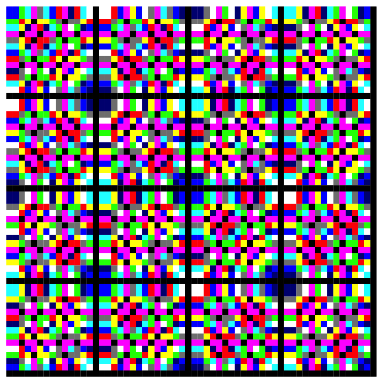
Letzte Ziffer, Multiplikation
Letzte Ziffer, Addition
4 Weitere Beispiele
Es geht natźrlich auch mit anderen Modulzahlen m.
4.1 Modulo 7
Fźr 
ergibt sich die
PeriodenlŠnge 16 und folgendes Muster:
modulo 7, Multiplikation
modulo 7, Addition
4.2 Modulo 3
Fźr 
ergibt sich die
PeriodenlŠnge 8 und, mit verŠnderter Farbcodierung, das Muster:
modulo 3, Multiplikation
modulo 3, Addition
5 Hintergrund
Die
Fibonacci-Zahlen modulo m sind
periodisch. Dies kann mit dem Schubfach-Prinzip von Dirichlet eingesehen
werden: Nach spŠtestens 
Schritten wiederholt
sich das Startwertepaar. Also ist die PeriodenlŠnge hšchstens 
. Wie unsere Beispiele zeigen, ist die PeriodenlŠnge in der Regel kźrzer.
Da die Multiplikation und die Addition kommutativ sind, ergeben sich symmetrische Bilder; wir haben eine Symmetrieachse von links oben nach rechts unten.