Hans Walser, [20090524b]

Schnecke von Fibonacci

1 Worum es geht

Die Fibonacci-Rekursion wird verallgemeinert und auf Vektoren in der Ebene angewandt. Es entstehen Kreise und logarithmische Spiralen.

Da die Fibonacci-Rekursion (auch die von uns verwendete verallgemeinerte Rekursion) linear ist, sind alle Folgevektoren Linearkombinationen der beiden Startvektoren. Die Figur liegt also in der durch die beiden Startvektoren aufgespannten Ebene. Daher können wir uns auf Vektoren in der Ebene beschränken.

Beispiel: Wir arbeiten mit der Rekursion:

Mit den Startvektoren und ergeben sich die folgenden Vektoren, deren Spitzen auf einer logarithmischen Spirale liegen:

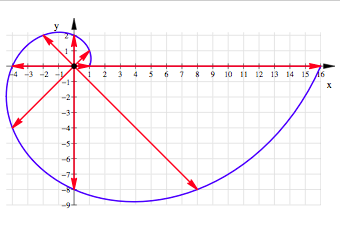
Logarithmische Spirale

Warum geht das so?

2 Kreise

2.1 Die Rekursion

Wir wählen zwei beliebige Ortsvektoren und gleicher Länge als Startvektoren. Weiter sei:

Dieser Wert p ist also der Kosinus des Zwischenwinkels der beiden Startvektoren. Nun bilden wir eine Vektorenfolge mit der verallgemeinerten Fibonacci-Rekursion:

2.2 Beispiel

Wir wählen und . Damit ist , und wir haben die Rekursion:

Es sei der Endpunkt des Ortsvektors . Das sieht dann so aus:

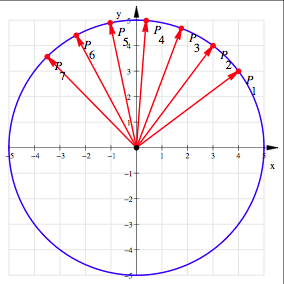
Die ersten sieben Vektoren

Offensichtlich sind die Vektoren gleich lang und haben gleiche Zwischenwinkel.

Der Beweis ergibt sich unmittelbar aus folgender Figur.

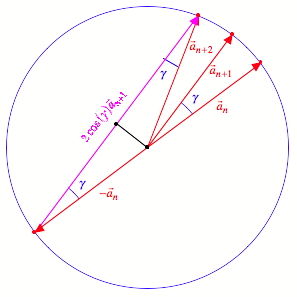
Beweisfigur

In der Regel geht es aber nicht „auf“:

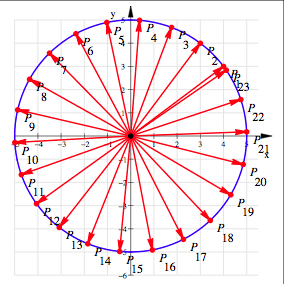
Es geht nicht auf

„Aufgehen“ tut es genau dann, wenn der Zwischenwinkel in einem rationalen Verhältnis zu steht.

2.3 Sieben

2.3.1 Regelmäßiges Siebeneck

Wir wählen und 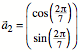. Es ist also . Damit erhalten wir ein regelmäßiges Siebeneck.

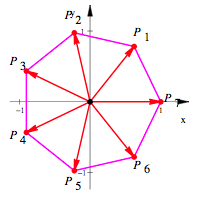
Regelmäßiges Siebeneck

2.3.2 Siebenstern

Wir wählen und 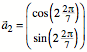. Es ist also . Damit erhalten wir einen regelmäßigen Siebenstern.

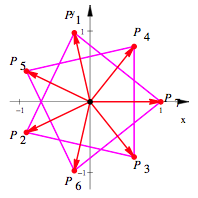
Siebenstern

2.3.3 Noch ein Siebenstern

Wir wählen und 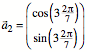. Es ist also . Damit erhalten wir einen anderen regelmäßigen Siebenstern.

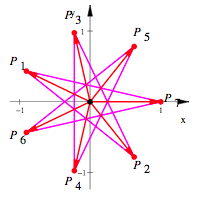
Ein anderer Siebenstern

2.3.4 Und noch einer

Wir wählen und 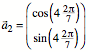. Es ist also . Damit erhalten wir einen regelmäßigen Siebenstern, der zwar gleich aussieht, aber einen anderen Eckendurchlauf hat.

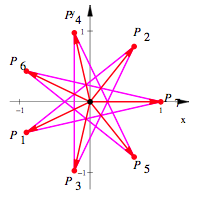
Ecken in anderer Reihenfolge durchlaufen

2.4 Ungleich lange Startvektoren

Was ergibt sich, wenn die beiden Startvektoren und nicht die gleiche Länge haben?

2.4.1 Das Linsengericht

Wir versuchen es mit den Startvektoren und . Gegenüber dem Eingangsbeispiel ist nun auch der Zwischenwinkel und damit das p verändert. Das sieht dann so aus:

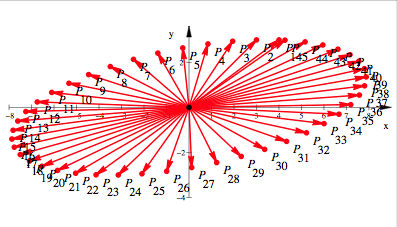
Versuch

Wir wetten ein Linsengericht, dass das nun eine Ellipse ist. Allerdings sehen wir, dass es in diesem Beispiel nicht „aufgeht“.

2.4.2 Beweis

Wir normieren die beiden Startvektoren auf die Länge 1. Wir machen das mit einer linearen Abbildung, welche die beiden Startvektoren als Eigenvektoren und deren Längen als Kehrwerte der zugehörigen Eigenwerte hat. Nun sind wir in der Lage gleich langer Startvektoren, wo sich ein Kreis (nun sogar der Einheitskreis) ergibt. Rückabbildung ergibt eine Ellipse, da die Rekursion linear und damit affin invariant ist.

Man beachte, dass der maßgebliche Winkel zwischen den Startvektoren nicht verändert wird, wohl aber die anderen Zwischenwinkel.

„Aufgehen“ tut es also nach wie vor genau dann, wenn der Winkel zwischen den Startvektoren in einem rationalen Verhältnis zum vollen Winkel steht.

2.4.3 Ein affin reguläres Achteck

Wir verwenden die Startvektoren und . Für den Zwischenwinkel finden wir:

Somit ist , und es sollte nach 8 Schritten aufgehen. Wir erhalten die Figur:

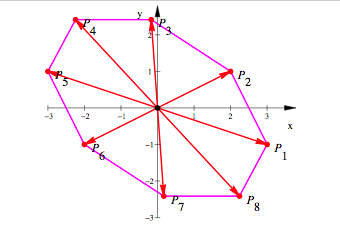
Affin reguläres Achteck

Eine Figur, die mit einer linearen Abbildung aus einem regelmäßigen Achteck hervorgeht, wir als affin reguläres Achteck bezeichnet.

3 Spiralen

Wir ändern die Rekursion etwas ab. Beginnen tun wir wieder mit zwei beliebigen Startvektoren und . Damit berechnen wir die Werte:

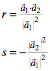
Wir verwenden nun die Rekursion:

3.1 Beispiel

Mit den Startvektoren und erhalten wir folgende Figur.

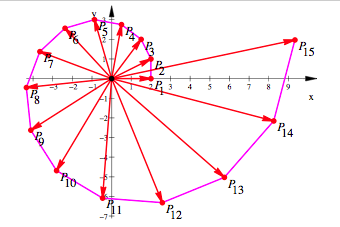
Spirale

Es dürfte sich um eine logarithmische Spirale handeln.

3.2 Beweis

Wenn wir den Startvektor mit dem Faktor auf die Länge des zweiten Startvektors normieren, erhalten wir mit der eingangs verwendeten Rekursion

einen weiteren Fächervektor gleicher Länge im gleichen Winkelabstand (Situation des Kreises). Nun multiplizieren wir diesen Vektor mit dem Faktor . Damit haben wir drei aufeinander folgende Vektoren mit dem gleichen Winkelabstand, aber exponentiell wachsender Länge. Die Spitzen liegen auf einer logarithmischen Spirale. Für die Rekursion heißt das:

3.3 Weiteres Beispiel

Die Frage des „Aufgehens“ ist wieder eine Frage des Zwischenwinkels. Mit den Startvektoren und , welche den Zwischenwinkel 45° haben, ergibt sich:

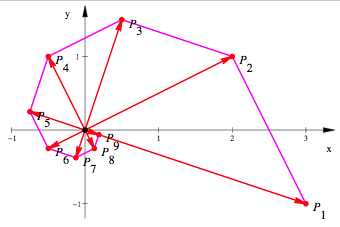
Schnecke