Hans Walser, [20150820]

Fibonacci triangle

1 The triangle

Figure 1 gives the Fibonacci triangle.

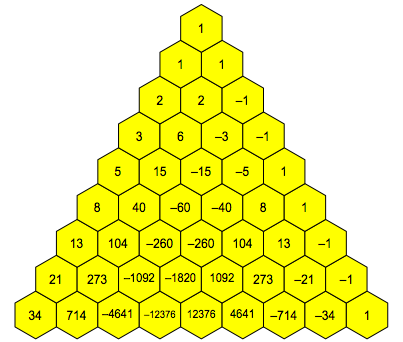
Fig. 1: Fibonacci triangle

In Figure 2 we see an orthogonal arrangement.

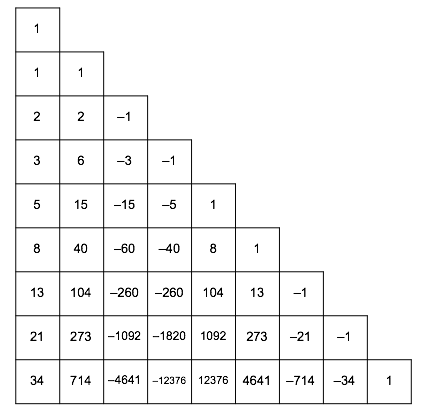
Fig. 2: Orthogonal arrangement

2 Notation

For the Fibonacci numbers we use the usual upper case notation:

(1)

For the Fibonacci triangle we will use the lower case notation of Figure 3.

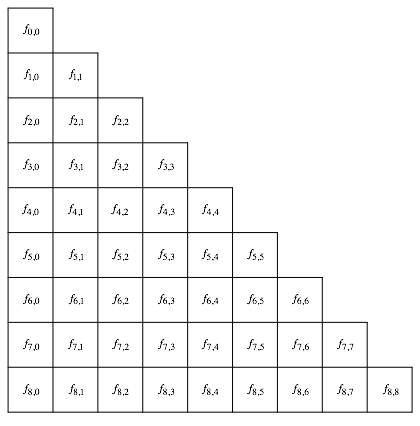
Fig. 3: Notation

3 Features of the Fibonacci triangle

3.1 The Fibonacci numbers

The numbers in the first column of Figure 2 are the usual Fibonacci numbers:

(2)

The Fibonacci numbers appear also under the roof:

(3)

3.2 Signs

The signs change every second step (Fig. 4).

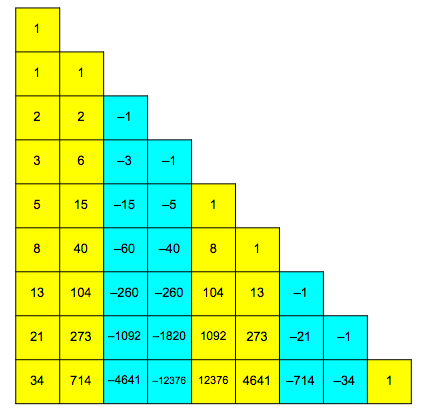
Fig. 4: Signs

3.3 Symmetry

The Fibonacci triangle is not symmetric. But leaving away the “roof” on the right and ignoring the signs there is an axial symmetry (Fig. 5).

Fig. 5: Quasi symmetry

4 Powers of the Fibonacci numbers

4.1 Squares and cubes

Lets begin with a common picture (Fig. 6). It depicts the growth of the Fibonacci numbers. Beginning with a unit square we get the Fibonacci numbers for the side lengths of the square sequence. And of course we have the recursion:

(4)

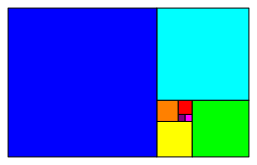
Fig. 6: Fibonacci squares

For the areas of the squares we obtain the sequence :

1, 1, 4, 9, 25, 64, 169, 441, 1156, ... (5)

Playing with these numbers we find a three digits recursion:

(6)

Example:

(7)

That means, that in Figure 6 the green and the cyan square have together half the area of the yellow plus the blue square. This can be seen by the dissection proof of Figure 7.

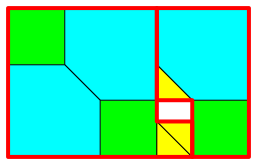
Fig. 7: Dissection

Notice that the coefficients of (6) appear in the Fibonacci triangle:

(8)

For the cubes of the Fibonacci numbers we have:

1, 2, 8, 27, 125, 512, 2197, 9261, 39304, ... (9)

Here we find a four digits recursion:

(10)

Example:

(11)

4.2 General powers

For the kth power of the Fibonacci numbers there is a (k + 1) digits recursion:

(12)

For the proof of (12) I used a computer algebra system.

5 The elements of the Fibonacci triangle

5.1 Columns

We have already found (2) the Fibonacci numbers in the first column of Figure 2.

In the next column of Figure 2 we have the products of two consecutive Fibonacci numbers:

(13)

Example:

(14)

Again in the next column we get products of three consecutive Fibonacci numbers, but with a negative sign an a coefficient of one half:

(15)

Example:

(16)

5.2 Overview

For the first five columns we get:

The denominators in the coefficients are the products of consecutive Fibonacci numbers beginning with (kind of “factorial”):

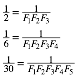(17)

5.3 General

Finally we get the general formula for the elements of the Fibonacci triangle:

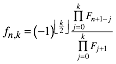(18)

6 Recursion in the Columns

The elements in the columns of the Fibonacci triangle fulfill a recursion like the recursion (12) for the powers of the Fibonacci numbers. Id est:

(19)

Examples:

First example: n = 7, k = 1

(20)

Figure 8 shows the involved elements. Red is the dot product of cyan and yellow.

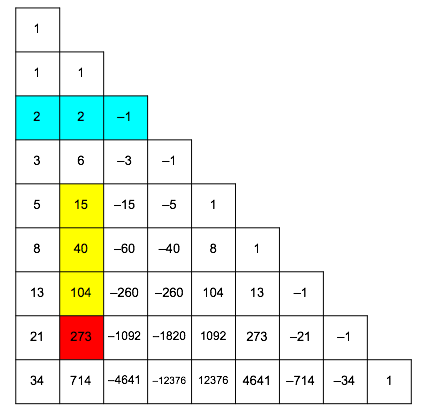
Fig. 8: Dot product

Second example: n = 8, k = 2

In Figure 9 the involved elements:

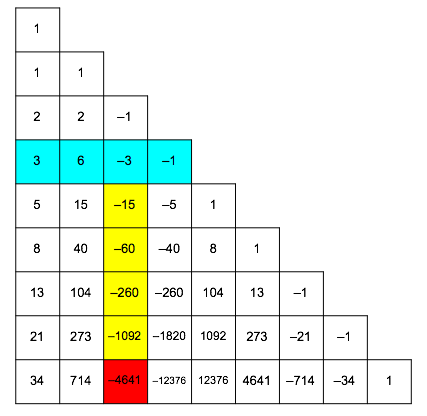
Fig. 9: Involved elements