Hans Walser, [20230617]
Fibonacci trifft Pythagoras
Anregung: Thomas Jahre, Aufgabe 63 – 754
1 Worum es geht
Spezielle Folgen von pythagoreischen Dreiecken.
Link zwischen pythagoreischen Dreiecken und klassischen rechtwinkligen Dreiecken mit irrationalem Seitenverhältnis.
2 Fast gleichschenklige pythagoreische Dreiecke
2.1 Ausgangslage
Ein gleichschenklig-rechtwinkliges Dreieck hat das irrationale Seitenverhältnis 1:1:sqrt(2). Es ist kein pythagoreisches Dreieck.
Hingegen sind beim pythagoreischen Dreieck mit dem Seitenverhältnis 3:4:5 (ägyptisches Dreieck, Abb. 1) die beiden Katheten fast gleich lang. Sie unterscheiden sich nur um 1.
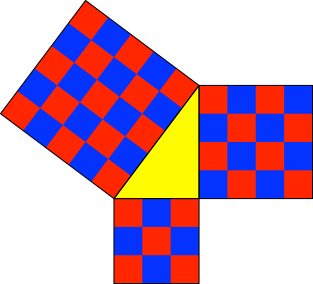
Abb. 1: Fast gleichschenkliges pythagoreisches Dreieck
Beim pythagoreischen Dreieck mit dem Seitenverhältnis 20:21:29 (Chemnitzer-Dreieck) sind die beiden Katheten ebenfalls fast gleich lang. Sie unterscheiden sich nur um 1.
Gibt es weitere fast gleichschenklige pythagoreische Dreiecke?
2.2 Verallgemeinerte Fibonacci-Folge
Wir konstruieren die verallgemeinerte Fibonacci-Folge mit den Startwerten
u[0] := 1:
u[1] := 2:
und der Rekursion:
u[n] := 2*u[n-1] + u[n-2]:
Der Faktor 2 in der Rekursion ist die einzige Abweichung gegenüber der üblichen Fibonacci-Folge.
Die Tabelle 1 zeigt die ersten Folgenglieder. Wir erkennen die Hypotenusenlängen der beiden oben angegebenen Beispiele von fast gleichschenkligen pythagoreischen Dreiecken.
|
n |
u[n] |
|
0 |
1 |
|
1 |
2 |
|
2 |
5 |
|
3 |
12 |
|
4 |
29 |
|
5 |
70 |
|
6 |
169 |
|
7 |
408 |
|
8 |
985 |
|
9 |
2378 |
|
10 |
5741 |
Tab. 1: Folgenglieder
2.3 Berechnung der Dreiecksseiten
Wir definieren:
a[n] := u[n]^2 - u[n-1]^2:
b[n] := 2*u[n]*u[n-1]:
c[n] := u[n]^2 + u[n-1]^2:
Es handelt sich hier um die übliche Parametrisierung der pythagoreischen Dreiecke.
Die Tabelle 2 zeigt die zugehörigen Werte.
|
n |
u[n] |
u[n-1] |
a[n] |
b[n] |
c[n] |
|
1 |
2 |
1 |
3 |
4 |
5 |
|
2 |
5 |
2 |
21 |
20 |
29 |
|
3 |
12 |
5 |
119 |
120 |
169 |
|
4 |
29 |
12 |
697 |
696 |
985 |
|
5 |
70 |
29 |
4059 |
4060 |
5741 |
|
6 |
169 |
70 |
23661 |
23660 |
33461 |
|
7 |
408 |
169 |
137903 |
137904 |
195025 |
|
8 |
985 |
408 |
803761 |
803760 |
1136689 |
|
9 |
2378 |
985 |
4684659 |
4684660 |
6625109 |
|
10 |
5741 |
2378 |
27304197 |
27304196 |
38613965 |
Tab. 2: Fast gleichschenklige pythagoreische Dreiecke
Der Quotient
c[n]/a[n] strebt für wachsendes n gegen √2 (Tab. 3).
|
n |
u[n] |
u[n-1] |
a[n] |
b[n] |
c[n] |
c[n]/a[n] |
|
1 |
2 |
1 |
3 |
4 |
5 |
1.666666667 |
|
2 |
5 |
2 |
21 |
20 |
29 |
1.380952381 |
|
3 |
12 |
5 |
119 |
120 |
169 |
1.420168067 |
|
4 |
29 |
12 |
697 |
696 |
985 |
1.413199426 |
|
5 |
70 |
29 |
4059 |
4060 |
5741 |
1.414387780 |
|
6 |
169 |
70 |
23661 |
23660 |
33461 |
1.414183678 |
|
7 |
408 |
169 |
137903 |
137904 |
195025 |
1.414218690 |
|
8 |
985 |
408 |
803761 |
803760 |
1136689 |
1.414212683 |
|
9 |
2378 |
985 |
4684659 |
4684660 |
6625109 |
1.414213713 |
|
10 |
5741 |
2378 |
27304197 |
27304196 |
38613965 |
1.414213536 |
Tab. 3: Quotient
3 Fibonacci trifft Pythagoras
Natürlich fragt man sich, was geschieht, wenn wir mit der üblichen Fibonacci-Folge arbeiten.
3.1 Fibonacci-Folge
Startwerte:
u[0] := 1:
u[1] := 2:
Rekursion:
u[n] := u[n-1] + u[n-2]:
Fibonacci-Folge (Tab. 4).
|
n |
u[n] |
|
0 |
1 |
|
1 |
2 |
|
2 |
3 |
|
3 |
5 |
|
4 |
8 |
|
5 |
13 |
|
6 |
21 |
|
7 |
34 |
|
8 |
55 |
|
9 |
89 |
|
10 |
144 |
Tab. 4: Fibonacci-Folge
3.2 Dreiecksseiten
Wir definieren wiederum:
a[n] := u[n]^2 - u[n-1]^2:
b[n] := 2*u[n]*u[n-1]:
c[n] := u[n]^2 + u[n-1]^2:
Die Tabelle 5 zeigt die zugehörigen Werte.
|
n |
u[n] |
u[n-1] |
a[n] |
b[n] |
c[n] |
b[n]/a[n] |
c[n]/a[n] |
|
1 |
2 |
1 |
3 |
4 |
5 |
1.333333333 |
1.666666667 |
|
2 |
3 |
2 |
5 |
12 |
13 |
2.400000000 |
2.600000000 |
|
3 |
5 |
3 |
16 |
30 |
34 |
1.875000000 |
2.125000000 |
|
4 |
8 |
5 |
39 |
80 |
89 |
2.051282051 |
2.282051282 |
|
5 |
13 |
8 |
105 |
208 |
233 |
1.980952381 |
2.219047619 |
|
6 |
21 |
13 |
272 |
546 |
610 |
2.007352941 |
2.242647059 |
|
7 |
34 |
21 |
715 |
1428 |
1597 |
1.997202797 |
2.233566434 |
|
8 |
55 |
34 |
1869 |
3740 |
4181 |
2.001070091 |
2.237025147 |
|
9 |
89 |
55 |
4896 |
9790 |
10946 |
1.999591503 |
2.235702614 |
|
10 |
144 |
89 |
12815 |
25632 |
28657 |
2.000156067 |
2.236207569 |
Tab. 5: Pythagoreische Dreiecke
3.3 Grenzdreieck
Für wachsende n streben die pythagoreischen Dreiecke gegen das rechtwinklige Dreieck mit dem irrationalen Seitenverhältnis 1:2:√5 (Abb.2).

Abb. 2: Grenzdreieck
Dies ist das Grunddreieck für viele Konstruktionen im Umfeld des Goldenen Schnittes.
Weblinks
Thomas Jahre: Aufgabe der Woche
https://www.schulmodell.eu/aufgabe-der-woche.html
Hans Walser: Fast gleichschenklige pythagoreische Dreiecke
Hans Walser: Fibonacci trifft Pythagoras
http://www.walser-h-m.ch/hans/Miniaturen/F/Fibo_Pyth/Fibo_Pyth.htm