Hans Walser, [20090411a]
Fibonacci, Kreisfunktionen und hyperbolische Funktionen
Spezielle verallgemeinerte Fibonacci-Rekursionen fhren
auf Kreis- und Hyberbelfunktionen.
1
Fibonacci und Kreisfunktionen
1.1
Einstiegsbeispiel
Wir untersuchen die Folge mit der Rekursion
![]()
und den Startwerten ![]() und
und ![]() . Excel liefert fr die ersten 50 Folgenglieder:
. Excel liefert fr die ersten 50 Folgenglieder:
|
n |
a_n |
n |
a_n |
n |
a_n |
|
0 |
1 |
17 |
0.633554136 |
34 |
-0.197218313 |
|
1 |
0.95 |
18 |
0.843463666 |
35 |
0.118759788 |
|
2 |
0.805 |
19 |
0.969026829 |
36 |
0.422861911 |
|
3 |
0.5795 |
20 |
0.997687309 |
37 |
0.684677842 |
|
4 |
0.29605 |
21 |
0.926579058 |
38 |
0.878025989 |
|
5 |
-0.017005 |
22 |
0.762812901 |
39 |
0.983571538 |
|
6 |
-0.3283595 |
23 |
0.522765455 |
40 |
0.990759932 |
|
7 |
-0.60687805 |
24 |
0.230441462 |
41 |
0.898872333 |
|
8 |
-0.824708795 |
25 |
-0.084926676 |
42 |
0.717097501 |
|
9 |
-0.960068661 |
26 |
-0.391802147 |
43 |
0.463612919 |
|
10 |
-0.999421660 |
27 |
-0.659497403 |
44 |
0.163767045 |
|
11 |
-0.938832493 |
28 |
-0.861242919 |
45 |
-0.152455534 |
|
12 |
-0.784360078 |
29 |
-0.976864143 |
46 |
-0.453432559 |
|
13 |
-0.551451654 |
30 |
-0.994798953 |
47 |
-0.709066328 |
|
14 |
-0.263398065 |
31 |
-0.913253867 |
48 |
-0.893793465 |
|
15 |
0.050995331 |
32 |
-0.740383395 |
49 |
-0.989141255 |
|
16 |
0.360289193 |
33 |
-0.493474583 |
50 |
-0.985574919 |
Das zugehrige Sulendiagramm lsst eine Kosinuskurve erkennen:
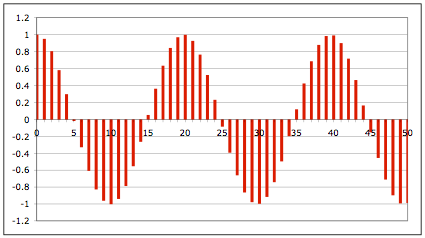
Diagramm. Kosinuskurve
1.2
Rekursion und Startwerte
Wir untersuchen Folgen mit der Rekursion:
![]()
Mit den Startwerten ![]() und
und ![]() ergibt sich eine
Folge, deren Werte auf einer Kosinuskurve liegen. Mit derselben Rekursion, aber
den Startwerten
ergibt sich eine
Folge, deren Werte auf einer Kosinuskurve liegen. Mit derselben Rekursion, aber
den Startwerten ![]() und
und ![]() ergibt sich eine
Folge, deren Werte auf einer Sinuskurve liegen.
ergibt sich eine
Folge, deren Werte auf einer Sinuskurve liegen.
Beispiel: ![]() . Startwerte
. Startwerte ![]() und
und ![]() .
.
|
n |
a_n |
n |
a_n |
n |
a_n |
|
0 |
0 |
17 |
-0.773698363 |
34 |
-0.980359596 |
|
1 |
0.3122499 |
18 |
-0.537186229 |
35 |
-0.992923014 |
|
2 |
0.59327481 |
19 |
-0.246955472 |
36 |
-0.906194132 |
|
3 |
0.814972239 |
20 |
0.067970832 |
37 |
-0.728845836 |
|
4 |
0.955172444 |
21 |
0.376100052 |
38 |
-0.478612956 |
|
5 |
0.999855405 |
22 |
0.646619268 |
39 |
-0.180518781 |
|
6 |
0.944552825 |
23 |
0.852476557 |
40 |
0.135627272 |
|
7 |
0.794794963 |
24 |
0.973086190 |
41 |
0.438210598 |
|
8 |
0.565557604 |
25 |
0.996387204 |
42 |
0.696972864 |
|
9 |
0.279764485 |
26 |
0.920049497 |
43 |
0.886037844 |
|
10 |
-0.034005082 |
27 |
0.751706841 |
44 |
0.986499040 |
|
11 |
-0.344374141 |
28 |
0.508193501 |
45 |
0.988310331 |
|
12 |
-0.620305787 |
29 |
0.213860811 |
46 |
0.891290589 |
|
13 |
-0.834206853 |
30 |
-0.101857960 |
47 |
0.705141789 |
|
14 |
-0.964687234 |
31 |
-0.407390936 |
48 |
0.448478809 |
|
15 |
-0.998698892 |
32 |
-0.672184818 |
49 |
0.146967949 |
|
16 |
-0.932840660 |
33 |
-0.869760218 |
50 |
-0.169239706 |
Das zugehrige Sulendiagramm lsst eine Sinuskurve erkennen:
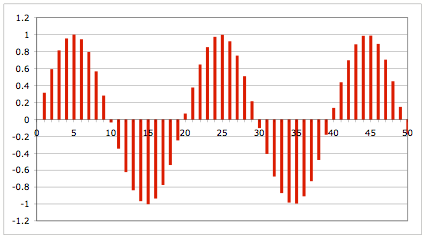
Diagramm. Sinuskurve
1.3
Beweis
Wir untersuchen den Fall ![]() mit den
Startwerten
mit den
Startwerten ![]() und
und ![]() , und setzen
, und setzen ![]() . Wir haben also die Rekursion
. Wir haben also die Rekursion
![]()
und die Startwerte ![]() sowie
sowie ![]() .
.
Dann gilt:
![]()
Beweis induktiv. Die Startwerte erfllen die Behauptung.
Weiter ist:
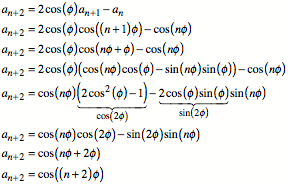
Damit ist die Behauptung bewiesen.
Im Fall ![]() mit den
Startwerten
mit den
Startwerten ![]() und
und ![]() setzen wir wieder
setzen wir wieder
![]() . Wir haben also dieselbe Rekursion
. Wir haben also dieselbe Rekursion
![]()
und die Startwerte ![]() sowie
sowie ![]() . Dann gilt:
. Dann gilt:
![]()
Der Beweis luft analog.
1.4
Periodenlnge
Fr die Periodenlnge T der so generierten Kreisfunktionen gilt:
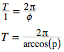
In unserem
Beispiel mit ![]() erhalten wir:
erhalten wir:
![]()
Aus den Diagrammen lesen wir eine Periodenlnge von etwa
20 ab.
1.5
Noch ein Beispiel
Wir verwenden einen negativen Wert fr p. Startwerte ![]() und
und ![]() .
.
Beispiel: ![]()
|
n |
a_n |
n |
a_n |
n |
a_n |
|
0 |
1 |
17 |
0.741547963 |
34 |
0.099786763 |
|
1 |
-0.99 |
18 |
-0.828774555 |
35 |
-0.239152167 |
|
2 |
0.9602 |
19 |
0.899425656 |
36 |
0.373734526 |
|
3 |
-0.911196 |
20 |
-0.952088244 |
37 |
-0.500842196 |
|
4 |
0.84396808 |
21 |
0.985709066 |
38 |
0.617933021 |
|
5 |
-0.759860798 |
22 |
-0.999615708 |
39 |
-0.722665186 |
|
6 |
0.660556301 |
23 |
0.993530035 |
40 |
0.812944047 |
|
7 |
-0.548040677 |
24 |
-0.967573762 |
41 |
-0.886964027 |
|
8 |
0.424564240 |
25 |
0.922266013 |
42 |
0.943244727 |
|
9 |
-0.292596518 |
26 |
-0.858512944 |
43 |
-0.980660532 |
|
10 |
0.154776866 |
27 |
0.777589617 |
44 |
0.998463127 |
|
11 |
-0.013861676 |
28 |
-0.681114496 |
45 |
-0.996296459 |
|
12 |
-0.127330747 |
29 |
0.571017086 |
46 |
0.974203862 |
|
13 |
0.265976555 |
30 |
-0.449499335 |
47 |
-0.932627187 |
|
14 |
-0.399302832 |
31 |
0.318991596 |
48 |
0.872397969 |
|
15 |
0.524643053 |
32 |
-0.182104026 |
49 |
-0.794720792 |
|
16 |
-0.639490412 |
33 |
0.041574375 |
50 |
0.701149198 |
Das Diagramm sieht lustig aus:
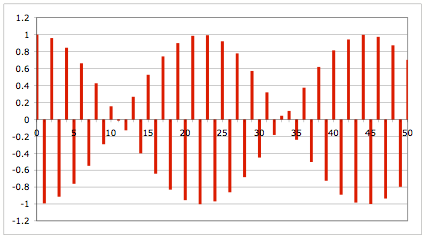
Diagramm
Wir haben einen Flipflop-Effekt. Es ist aber immer noch ![]() . — Und nicht, wie der Schreiber dieses zuerst
vermutete,
. — Und nicht, wie der Schreiber dieses zuerst
vermutete, ![]() .
.
Die Periodenlnge ist viel krzer, als man denkt:
![]()
Wie ist das zu verstehen?
1.6
Andere Startwerte
Beispiel: ![]() , Startwerte
, Startwerte ![]() und
und ![]() . Wir erhalten
das Diagramm:
. Wir erhalten
das Diagramm:
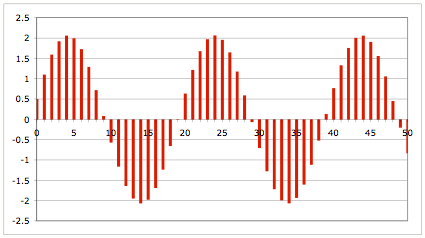
Diagramm
Wir haben eine Linearkombination einer Kosinusfunktion und
einer Sinusfunktion.
2
p > 1
Bis jetzt war ![]() , und das war ja auch gut so, weil wir in unseren
berlegungen mit
, und das war ja auch gut so, weil wir in unseren
berlegungen mit ![]() gearbeitet
haben, was fr
gearbeitet
haben, was fr ![]() nicht ginge.
Allerdings knnen wir gleichwohl mit der Rekursion
nicht ginge.
Allerdings knnen wir gleichwohl mit der Rekursion ![]() und den
Startwerten
und den
Startwerten ![]() und
und ![]() arbeiten.
arbeiten.
2.1
Beispiel
Im Beispiel ![]() erhalten wir
erhalten wir
|
n |
a_n |
n |
a_n |
n |
a_n |
|
0 |
1 |
6 |
1.381452339 |
12 |
2.816821131 |
|
1 |
1.01 |
7 |
1.530392924 |
13 |
3.218329769 |
|
2 |
1.0402 |
8 |
1.709941367 |
14 |
3.684205002 |
|
3 |
1.091204 |
9 |
1.923688637 |
15 |
4.223764334 |
|
4 |
1.16403208 |
10 |
2.175909680 |
16 |
4.847798954 |
|
5 |
1.260140802 |
11 |
2.471648916 |
|
|
mit dem Diagramm:
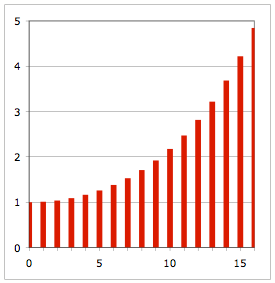
Diagramm
Das schmeckt sehr nach hyperbolischem Kosinus.
Tatschlich gilt: mit ![]() wird
wird ![]() .
.
Und mit den Startwerten ![]() und
und ![]() ergibt sich
ergibt sich ![]() . Die Beweise laufen analog zu denen der Kreisfunktionen, wobei
der Leser / die Leserin gut tut, vor dem Beweis die einschlgigen Formeln fr
die hyperbolischen Funktionen nachzusehen. — Wir haben damit ohne Wrgen
und Murksen einen Link von den Kreisfunktionen zu den hyperbolischen Funktionen
gefunden.
. Die Beweise laufen analog zu denen der Kreisfunktionen, wobei
der Leser / die Leserin gut tut, vor dem Beweis die einschlgigen Formeln fr
die hyperbolischen Funktionen nachzusehen. — Wir haben damit ohne Wrgen
und Murksen einen Link von den Kreisfunktionen zu den hyperbolischen Funktionen
gefunden.
2.2
p < –1
Im Beispiel ![]() erhalten wir
erhalten wir
|
n |
a_n |
n |
a_n |
n |
a_n |
|
0 |
1 |
6 |
1.381452339 |
12 |
2.816821131 |
|
1 |
-1.01 |
7 |
-1.530392924 |
13 |
-3.218329769 |
|
2 |
1.0402 |
8 |
1.709941367 |
14 |
3.684205002 |
|
3 |
-1.091204 |
9 |
-1.923688637 |
15 |
-4.223764334 |
|
4 |
1.16403208 |
10 |
2.175909680 |
16 |
4.847798954 |
|
5 |
-1.260140802 |
11 |
-2.471648916 |
|
|
mit dem Diagramm:
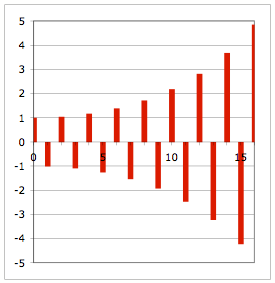
Diagramm
Hier kommt man wohl nicht darum herum, die Formel ![]() zu akzeptieren.
zu akzeptieren.
3
Hintergrund
3.1
Die Formel von Binet
Eine Folge mit der Rekursion ![]() und den Startwerten
und den Startwerten
![]() und
und ![]() kann explizit
dargestellt werden mit:
kann explizit
dargestellt werden mit:
![]()
Dabei ist:
![]()
Beweis induktiv mit einiger Rechnung.
In unserem Fall ist ![]() , also:
, also:
![]()
Weiter haben wir
![]()
und:
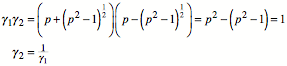
3.2
Spezielle Startwerte
Mit den speziellen Startwerten ![]() und
und ![]() erhalten wir:
erhalten wir:
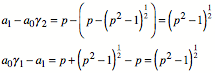
Eingesetzt in die explizite Formel von Binet liefert:
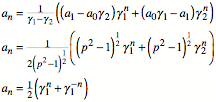
Das erinnert an die Definitionen von cos und cosh.
Wir machen nun eine Fallunterscheidung bezglich p.
3.2.1
|p| < 1
In diesem Fall ist:
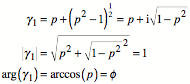
Es ist also:
![]()
Die explizite Formel von Binet wird zu:
![]()
3.2.2
p > 1
Hier ist:
![]()
Weiter ist:
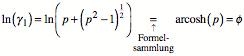
Die explizite Formel von Binet wird zu:
![]()