Hans Walser, [20150806], [20150810]

FlŠchenoptimierung im Viereck

Anregung: Chr. K., B.

1     Worum geht es

Wir beweisen den Satz:

Unter allen Vierecken mit gegebenen Seiten a, b, c, d hat das Sehnenviereck den grš§ten FlŠcheninhalt.

2     Beweis

Wir verwenden die Ÿblichen Bezeichnungen (Abb. 1) und unterteilen das Viereck mit der Diagonalen e in zwei Teildreiecke.

 

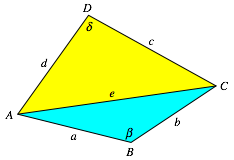
Abb. 1: Bezeichnungen. Unterteilung

 

FŸr den FlŠcheninhalt A des Viereckes gilt daher:

 

                                                                                 (1)

 

Nach dem Kosinussatz gilt fŸr die Diagonale e:

 

                                                                                               (2)

 

 

Somit haben wir die Nebenbedingung:

 

                                           (3)         

 

Wir haben die Funktion  unter der Nebenbedingung  zu optimieren.

Nach dem  Ÿblichen Verfahren bilden wir die Hilfsfunktion

 

                                                                                     (4)         

 

und setzen deren Gradienten null:

 

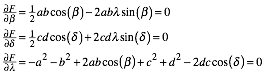                                                 (5)

 

 

Die ersten beiden Gleichungen lauten vereinfacht:

 

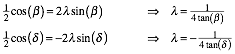                                                           (6)

 

 

Aus  folgt . Wir haben ein Sehnenviereck.

3     Bestimmung des Sehnenviereckes

Zu gegebenen vier Seiten ist ein Viereck bei Kenntnis eines Winkels bestimmt.

Wenn wir nun  in die Nebenbedingung  einsetzen, erhalten wir:

 

                                                                                                     (5)

 

Die Abbildung 2 zeigt das zu den SeitenlŠngen a, b, c, d des Viereckes der Abbildung 1 gehšrende Sehnenviereck.

 

Abb. 2: Sehnenviereck

 

4     Rechnereien

Wir berechnen weitere Daten des durch die vier Seiten a, b, c, d gegebenen Sehnenvierecks.

4.1    FlŠcheninhalt

Aus (7) ergibt sich durch Umrechnen auf Sinus:

 

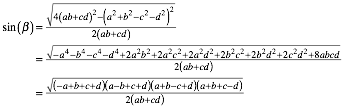                       (8)

 

 

 

Wegen  ist:

 

                                                                                                               (9)

 

Wir setzen (8) und (9) in (1) ein und erhalten fŸr den FlŠcheninhalt A:

 

                               (10)

 

Mit  (halber Umfang) kann die FlŠchenformel auch in der folgenden Form geschrieben werden:

 

                                                                                 (10a)

 

Das ist die Formel von Brahmagupta (598-670). FŸr d = 0 ergibt sich die Heronsche Formel fŸr die DreiecksflŠche.

4.2    Diagonalen

Wir setzen (5) in (2) ein und erhalten fŸr die Diagonale e:

 

                                                                                                       (11)

 

Durch zyklische Vertauschung ergibt sich fŸr die Diagonale f:

 

                                                                           (12)

 

Aus (11) und (12) ergibt sich:

 

                                                                                                         (13)

 

 

Dies ist der Satz von PtolemŠus.

4.3    Umkreisradius

FŸr den Umkreisradius r gilt im Dreieck ABC (Abb. 1):

 

                                                                                                                   (14)

 

Einsetzen von (8) und (11) liefert:

 

                     (15)

 

 

Isch dšs a Rechnerei!

5     Ausblick. Isoperimetrisches Problem

Es gilt:

Ein n-Eck mit gegebenen Seiten  hat genau dann maximalen FlŠcheninhalt,  wenn seine Ecken auf einem Kreis liegen (Sehnen-n-Eck).

Beweis: www.walser-h-m.ch/hans/Miniaturen/I/Isoper_Vielecke/Isoper_Vielecke.htm

Das ist eine diskrete Version des isoperimetrischen Problems.