Hans Walser, [20250104]

Flächengleiche Ellipsen

1 Worum es geht

Hüllkurve (Enveloppe) flächengleicher Ellipsen.

2 Flächengleiche Rechtecke

Wir beginnen mit einem Quadrat (Abb. 1). Für rechnerische Zwecke nehmen wir an, das Quadrat habe die Seitenlänge 2.

Abb. 1: Quadrat

Nun skalieren wir das Quadrat in der horizontalen Richtung mit dem Parameter t und in der vertikalen Richtung mit dem Parameter 1/t (Abb. 2). Es entstehen Rechtecke, die alle denselben Flächeninhalt haben.

Abb. 2: Skalierung

Die Ecken der Rechtecke laufen auf Hyperbeln (Abb. 3) mit den Gleichungen xy = ±1.

Abb. 3: Bahnkurven der Ecken sind Hyperbeln

3 Umkreis und Umellipsen

Zum Quadrat der Abbildung 1 zeichnen wir den Umkreis (Abb. 4).

Abb. 4: Umkreis

Wir skalieren nun die Figur in der horizontalen Richtung mit dem Parameter t und in der vertikalen Richtung mit dem Parameter 1/t (Abb. 5). Es entstehen Ellipsen, die alle denselben Flächeninhalt haben.

Abb. 5: Flächengleiche Ellipsen

4 Enveloppe

Die Ellipsenschar hat die Bahnkurven der Rechteckecken als Enveloppen (Einhüllende) (Abb. 6).

Abb. 6: Enveloppen

Die Ellipsen berühren also die Hyperbeln.

5 Beweis

Die Ellipsenschar kann beschrieben werden durch:

(1)

Wir setzen die Ableitung von f nach t gleich null:

(2)

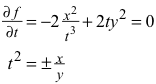
Elimination von t aus (1) und (2) führt auf die Hyperbelgleichungen ±xy = 1.