Hans Walser, [20130529]

FlŠchengleiche Rechtecke

1        Worum es geht

FlŠchengleiche Rechtecke und Parallelogramme sind zerlegungsgleich. Es werden einige Beispiele zum Auffinden der Zerlegungsgleichheit diskutiert.

2        FlŠchengleiche Rechtecke

FlŠchengleiche Rechtecke lassen sich mit der Gnomon-Konstruktion finden (Abb. 1). Die beiden grauen Rechtecke sind flŠchengleich.  

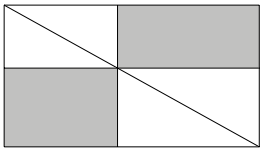
Abb. 1: Gnomon

3        Grundform der Zerlegung

Die Abbildung 2 zeigt die einfachste Form einer gemeinsamen Zerlegung.

Abb. 2: Zerlegungsgleichheit

Die entsprechenden Puzzle-Teile lassen sich durch eine Translation ineinander ŸberfŸhren. Jedes Rechteck ist punktsymmetrisch zerlegt.

Die Abbildung 3 zeigt eine Variante der Zerlegung, die zwar auch punktsymmetrisch ist, aber mehr Puzzle-Teile benštigt. Wir lassen diese Variante im Folgenden weg.

Abb. 3: Variante

4        Transposition

Nun transponieren wir eines der beiden Rechtecke. Transponieren hei§t, dass wir die Ma§e fŸr LŠnge und Breite vertauschen. Wir nehmen also eines der beiden Rechtecke im Hochformat. Dann ergibt sich eine andere gemeinsame Zerlegung (Abb. 4).

Abb. 4: Transponiertes Rechteck

Die Puzzle-Teile sind nicht mit denen der Abbildung 2 kompatibel, obwohl die beiden Rechtecke kongruent sind. Auch das Umrechteck fŸr die Gnomonkonstruktion hat andere Ausma§e.


5        Einbauen von Rechtecken

Die Abbildung 5 zeigt ein Beispiel, das zunŠchst ganz harmlos aussieht.

Abb. 5: Ein harmloses Beispiel

Wenn wir jedoch das eine Rechteck transponieren, kommen wir mit der Ÿblichen Konstruktion nicht mehr durch. Wir kšnnen das Problem auf verschiedene Weisen lšsen. In der Abbildung 6 sind zusŠtzliche rechtwinklige Dreiecke eingebaut worden.

Abb. 6: ZusŠtzliche Dreiecke

Die Dreiecke kšnnen teilweise zu Rechtecken zusammengefasst werden (Abb. 7).

Abb. 7: Rechtecke als Puzzle-Teile

NatŸrlich stšrt uns die fehlende Symmetrie. Dies kann mit Unterteilung der Rechtecke angegangen werden (Abb. 8).

Abb. 8: Symmetrische Zerlegungen

6        Rationale SeitenverhŠltnisse

Die Rechtecke der Abbildungen 1 und 2 haben die LŠngen 4cm und 5cm (Abb. 9). Diese LŠgen sind ein einem rationalen VerhŠltnis.

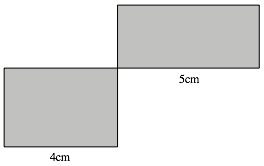
Abb. 9: Rationales VerhŠltnis

In diesem Fall gibt es eine gemeinsame Zerlegung ausschlie§lich durch Rechtecke, welche zu den Ausgangsrechtecken seitenparallel sind und durch Translationen ineinander ŸbergefŸhrt werden kšnnen.


6.1      Rechteckraster

Die Abbildung 10 zeigt eine Rasterlšsung. Wir haben formmŠ§ig nur ein Puzzle-Teil. FŸr jedes Rechteck benštigen wir 20 Puzzle-Teile.

Abb. 10: Rasterlšsung

Die Abbildung 11 zeigt die Rasterlšsung fŸr den transponierten Fall. Die Puzzle-Teile haben eine andere Form. Wir benštigen fŸr jedes Rechteck 45 Puzzle-Teile.

Abb. 11: Rasterlšsung fŸr den transponierten Fall

6.2      Rechtecke

Wenn wir mit Rechtecken verschiedener Grš§e arbeiten, brauchen wir insgesamt weniger Puzzle-Teile (Abb. 12).

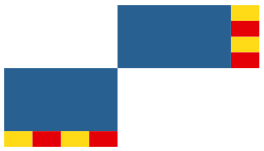
Abb. 12: Zerlegung in Rechtecke

Das funktioniert auch im transponierten Fall, aber die Puzzle-Rechtecke haben eine andere Form (Abb. 13). Auch die Anzahl der benštigten Puzzle-Teile ist anders.

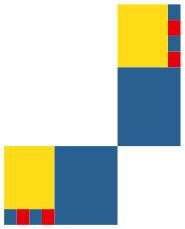
Abb. 13: Transponierte Version

6.3      Treppen

Die Abbildung 14 zeigt eine Treppenlšsung fŸr das Beispiel der Abbildung 12.

Abb. 14: Gru§ von James Joseph Sylvester

Wir benštigen lediglich zwei Puzzle-Teile. In der transponierten Version (vgl. Abb. 13) ist die Treppenlšsung weniger elegant (Abb. 15).

Abb. 15: Transponierte Version mit Treppe

6.4      US Letter

Wir vergleichen das US Letter-Format zwischen Querformat und Hochformat. Wegen den Ausma§en 11 in auf 8.5 in haben wir ein rationales VerhŠltnis. Eine Zerlegung mit translationsgleichen Rechtecken ist mšglich (Abb. 16).

Abb. 61: US Letter

7        DIN-Format

Das DIN-Format hat das irrationale SeitenverhŠltnis . Zwar kšnnen wir noch eine Zerlegung mit endlich vielen Dreiecken vornehmen (Abb. 17). Die gelben und roten Trapeze sind gleichschenklig und haben Basiswinkel von 45¡. Zudem ist die Deckparallele gleich lang wie die Schenkel.

Abb. 17: DIN-Format und Zerlegung

Eine Zerlegung mit translationsgleichen Rechtecken ist spannend. ZunŠchst kšnnen wir je ein Quadrat abschneiden (Abb. 18).

Abb. 18: Abschneiden von je einem Quadrat

Es bleiben dann zwei kongruente Restrechtecke mit den SeitenverhŠltnissen  beziehungsweise  Ÿbrig, eins im Hoch- und das andere im Querformat. Rechtecke mit diesem SeitenverhŠltnis werden als Silberne Rechtecke bezeichnet. Bei einem Silbernen Rechteck kšnnen wir zwei Quadrate abschneiden, aber das noch verbleibende Restrechteck ist wieder ein Silbernes Rechteck (Abb.19).

Abb. 19: Abschneiden je zweier Rechtecke

Das geht nun so weiter (Abb. 20).

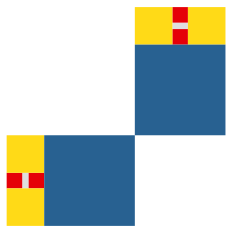
Abb. 20: NŠchster Schritt

Das Verfahren terminiert nicht. Wir erhalten eine unendliche Folge von Rechteckpaaren.

8        Parallelogramme

Unsere †berlegungen lassen sich auf Parallelogramme Ÿbertragen (Abb. 21).

Abb. 21: FlŠchengleiche Parallelogramme

In der Abbildung 22 ist eines der Parallelogramme transponiert worden.

Abb. 22: Transponiert

In der Abbildung 23 ist eines der Parallelogramme der Abbildung 21 verschoben worden.  Die Parallelogramme berŸhren sich  nun an einer stumpfen Ecke.

Abb. 23: BerŸhrung an stumpfer Ecke

Schlie§lich kšnnen wir auch hier transponieren (Abb. 24).

Abb. 24: BerŸhrung an stumpfer Ecke. Transponiert

Die Puzzle-Bauteile der Abbildungen 21 bis 24 sind alle verschieden, obwohl die Startparallelogramme kongruent sind.

9        Schiefe Rechtecke

Wir bearbeiten nun zwei zwar flŠchengleiche, aber nicht seitenparallele Rechtecke (Abb. 25).

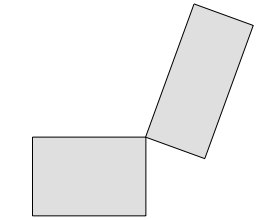
Abb. 25: FlŠchengleiche, aber schiefe Rechtecke

Die Idee ist, diese durch geeignetes Abschneiden und Ansetzen von Dreiecken in die Situation von zwei seitenparallelen Parallelogramme gemŠ§ Abbildungen 16 bis 19 zu bringen, darin die Zerlegung durchzufŸhren und schlie§lich das Abschneiden und Ansetzen geeignet rŸckgŠngig zu machen. Die Abbildung 26 zeigt zunŠchst das Abschneiden und Ansetzen. 

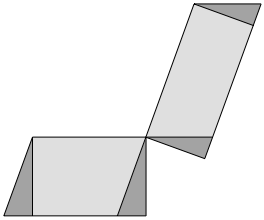
Abb. 26: Abschneiden und Ansetzen

Die Abbildung 27 zeigt das Resultat der Zerlegung. SŠmtliche entsprechende Puzzle-Teile kšnnen durch Translationen ineinander ŸbergefŸhrt werden.

Abb. 27: Zerlegung

Schšn und gut. Es fehlt allerdings die Symmetrie der Zerlegungen der einzelnen Rechtecke. Das erhalten wir, wenn wir das Abschneiden und Ansetzen punktsymmetrisch gestalten (Abb. 28). Dazu mŸssen wir die beiden Rechtecke etwas auseinanderrŸcken.

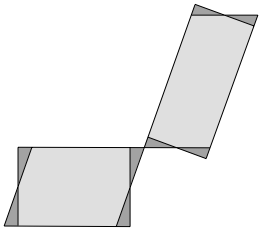
Abb. 28: Punktsymmetrisches Abschneiden und Ansetzen

Nun kšnnen wir eine punktsymmetrische Zerlegung anstellen (Abb. 29).

Abb. 29: Punktsymmetrische Zerlegung

Schlie§lich schneiden wir das AngefŸgte wieder ab (Abb. 30).

Abb. 30: Punktsymmetrische Rechteckzerlegung

Die Meinung, der ãDiagonalstreifenÒ sei geknickt, ist eine optische TŠuschung (Abb. 31). Wir haben das BedŸrfnis, das schrŠge Rechteck ãgeradezurŸckenÒ.

Abb. 31: Ist der gelbe Streifen geknickt?

Nun rŸcken wir die Rechtecke wieder zusammen (Abb. 32)

Abb. 32: Punktsymmetrische Rechteckzerlegung

Im Unterschied zu der Abbildung 32 ist der ãDiagonalstreifenÒ versetzt. Er ist aber nach wie vor nicht geknickt.


10    Kathetensatz

Schiefe flŠchengleiche Rechtecke kommen beim Kathetensatz vor, eines der beiden Rechtecke ist jeweils ein Quadrat (Abb. 33).

Abb. 33: Erinnerung an die Schule

Die Abbildung 34 zeigt die Zerlegung des roten Anteils.

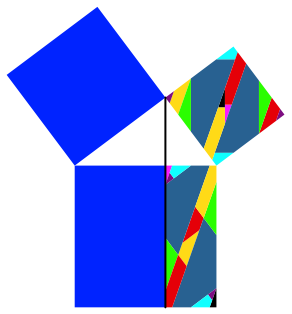
Abb. 34: Zerlegung des Anteils rechts

Die Abbildung 35 gibt beide Zerlegungen.

Abb. 35: Kathetensatz

Die Abbildung 36 zeigt eine Verallgemeinerung des Kathetensatzes auf beliebige Dreiecke. Rechtecke gleicher Farbe sind flŠchengleich.

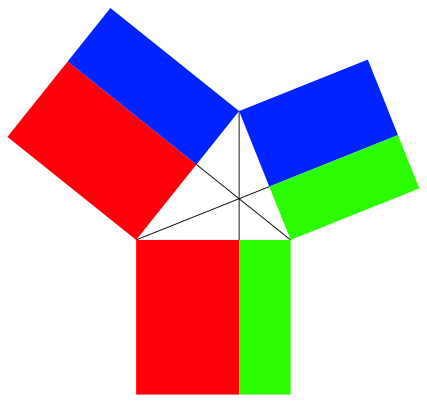
Abb. 36: FlŠchengleiche Rechtecke

In der Abbildung 37 die Zerlegung.

Abb. 37: Zerlegung

11    Ein falscher Zerlegungsbeweis

In der Abbildung 38 sehen wir ein Quadrat und ein Rechteck mit bei oberflŠchlichem Hinsehen gemeinsamer Zerlegung.

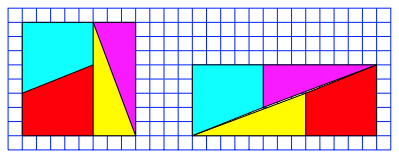
Abb. 38: Gemeinsame Zerlegung?

Das 8 mal 8 Quadrat hat einen FlŠcheninhalt von 64 Einheiten, das 13 mal 5 Rechteck aber einen FlŠcheninhalt von 65 Einheiten. Bei genauem Hinsehen erkennen wir, dass die Zerlegung nicht stimmt. Beim Rechteck haben wir eine offene Spalte.

Die in der Abbildung 38 auftretenden Ma§zahlen sind 3, 5, 8, 13. Das sind aufeinanderfolgende Fibonacci-Zahlen. Der Trick geht immer mit vier aufeinanderfolgenden Fibonacci-Zahlen. Die Abbildung 39 zeigt die Situation fŸr 5, 8, 13, 21. Nun ist 13 mal 13 gleich 169, hingegen 21 mal 8 nur 168. Das Rechteck hat eine Einheit verloren (durch †berlappung).

Abb. 39: Gemeinsame Zerlegung?

Zerlegungsbeweise sind also erst dann gŸltig, wenn nachgewiesen ist, dass alle Puzzle-Teile sich lŸckenlos und ohne †berlappung aneinanderfŸgen.