Hans Walser, [20210611]
FlŠchengleiche Rechtecke
1 Worum geht es?
Gemeinsame Zerlegung flŠchengleicher Rechtecke.
Sonderfall im goldenen Schnitt.
2 Es lŠuft wie auf Schienen
Die Abbildung 1a zeigt das Verfahren. Es funktioniert auch fźr flŠchengleiche Parallelogramme mit gleichen Winkeln (Abb. 1b).

Abb. 1: Zerlegungsgleichheit
Die entsprechenden Teile kšnnen alle mit einer Translation aufeinander abgebildet werden. Die Translationsrichtung ist immer dieselbe.
Bei ălangenŇ Rechtecken muss eine Salami-Taktik angewendet werden (Abb. 2).
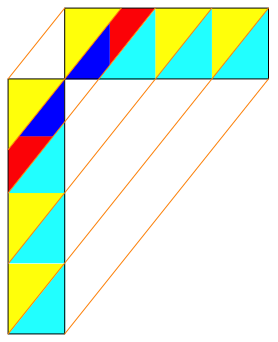
Abb. 2: Salami-Taktik
3 Sonderfall Goldener Schnitt
In der Abbildung 3 wird ein Quadrat mit einem flŠchengleichen Rechteck verglichen, dessen beide Seiten mit dem Goldenen Schnitt verlŠngert beziehungsweise verkźrzt wurden. Die Abbildung 3a zeigt das Verfahren gemŠ§ Abbildung 1.
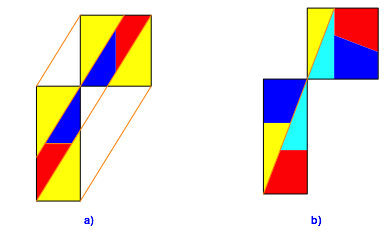
Abb. 3: Goldener Schnitt
Die Abbildung 3b zeigt ein anderes Verfahren. Wir haben nur bei zweien der vier Teile einen translatorischen Bezug. Die beiden anderen Teile mźssen um 90ˇ gedreht werden. Dieses Verfahren ist nicht auf beliebige flŠchengleiche Rechtecke anwendbar.
Der Hintergrund des Verfahrens der Abbildung 3b liegt darin, dass fźr die Potenzen des Goldenen Schnittes dieselbe Rekursion wie fźr die Fibonacci-Zahlen gilt.
Das Verfahren der Abbildung 3b ist (wegen der Drehungen um 90ˇ) nicht affin invariant. Es kann nicht auf Rhombus und Parallelogramm angewendet werden (Abb. 4b). Die Trapeze sind nicht mehr deckungsgleich.
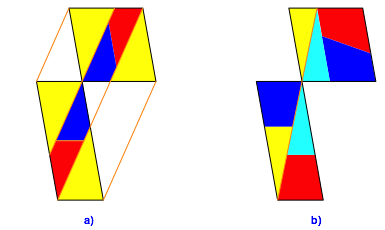
Abb. 4: Affine Verzerrung
Weblink
Hans Walser: FlŠchengleiche Rechtecke
http://www.walser-h-m.ch/hans/Miniaturen/F/Flaechengleiche_Rechtecke/Flaechengleiche_Rechtecke.htm