Hans Walser, [20130513]

FlŠchengleichheit

Anregung: H. K. S., L.

1        Worum es geht

Es wird mit regulŠren Vielecken gearbeitet, deren Eckenzahl ein Vielfaches von vier ist. Faktisch benštigen wir die HŠlfte oder einen Viertel eines solchen Vieleckes. Das Halbieren und Vierteln kann auf zwei Arten geschehen (Abb. 1 fŸr den Fall des regelmŠ§igen Achteckes).

 

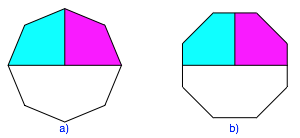
Abb. 1: Halbieren und Vierteln

 

In beiden FŠllen kšnnen wir eine Figur bauen, welche eine FlŠchengleichheit enthŠlt.

Die FlŠchengleichheit kann bei Polygonen mit Zerlegungen nachgewiesen werden. Spannend ist das Auffinden einer passenden und mšglichst einfachen Zerlegung.

2        Figuren mit FlŠchengleichheit

2.1      Basis regelmŠ§iges Achteck

Auf der Basis der Figuren der Abbildung 1a erhalten wir die Figur der Abbildung 2a, entsprechend auf der Basis der Figuren der Abbildung 1b die Figur der Abbildung 2b.  Die beiden FlŠchenanteile sind jeweils gleich gro§.

 

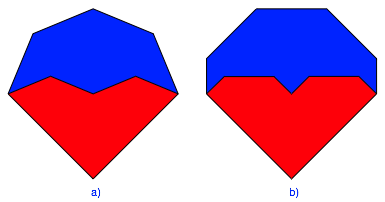
Abb. 2: Rot = Blau

 

Die FlŠchengleichheit kann nachgerechnet werden. Bei flŠchengleichen Polygonen gibt es aber immer auch eine Zerlegung, welche die FlŠchengleichheit nachweist. Die Abbildung 3 gibt mšgliche Zerlegungsbeweise fŸr die Figuren der Abbildung 2.

 

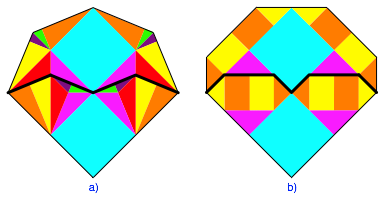
Abb. 3: Zerlegungsbeweise

 

Die auftretenden Rechtecke in der Abbildung 3b haben das SeitenverhŠltnis eines DIN-Rechteckes. Das ist beim regelmŠ§igen Achteck aber nicht erstaunlich.

2.2      Basis Quadrat

Die Abbildung 4 zeigt die beiden FŠlle auf der Basis eines Quadrates.

 

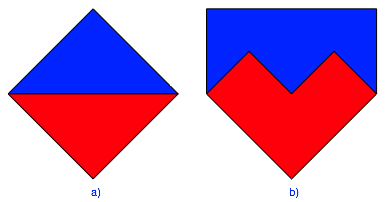
Abb. 4: Basis Quadrat

 

Die Zerlegungsgleichheiten sind offensichtlich (Abb. 5).

 

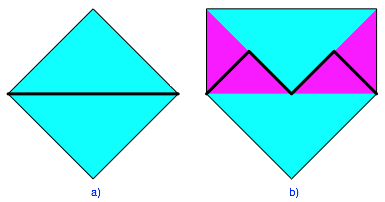
Abb. 5: Zerlegungsbeweise

 

2.3      Basis regelmŠ§iges Zwšlfeck

Die Abbildung 6 zeigt die beiden FŠlle auf der Basis eines regelmŠ§igen Zwšlfeckes.

 

Abb. 6: Basis Zwšlfeck

 

Die Abbildung 7 enthŠlt Zerlegungsbeweise fŸr die Figuren der Abbildung 6.

 

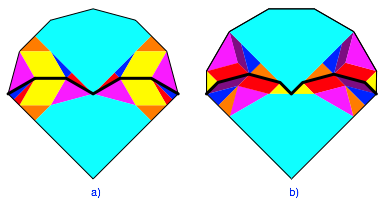
Abb. 7: Zerlegungsbeweise

 

3        Schiefe Halbierung

In der Abbildung 1 wurden als Trennlinien fŸr das Halbieren Symmetrieachsen des regulŠren Viereckes verwendet. RegulŠre Vielecke, deren Eckenzahl ein Vielfaches von vier ist, sind aber auch punktsymmetrisch. Wir kšnnen mit einer beliebigen Geraden durch das Symmetriezentrum halbieren. Die Abbildung 8a illustriert ein Beispiel fŸr das Quadrat. Das Quadrat ist gegenŸber der Horizontalen um 20¡ verdreht. Das ist kein ãschšnerÒ Winkel.

Die Abbildung 8b zeigt die zugehšrige Figur mit FlŠchenhalbierung. Sie ist asymmetrisch.

 

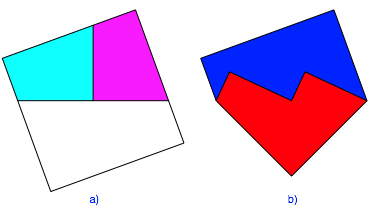
Abb. 8: Schiefe Halbierung

 

Entsprechend ist auch der Zerlegungsbeweis (Abb. 9) asymmetrisch.

 

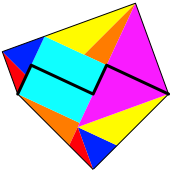
Abb. 9: Zerlegungsbeweis

 

4        Figur mit Kreisbšgen

Wenn wir mit der Eckenzahl gegen Unendlich fahren, erhalten wir das Kalenderblatt Dezember 2014 von Heinz Klaus Strick, Leverkusen (Abb. 10). In diesem Fall gibt es keinen Zerlegungsbeweis. Die FlŠchengleichheit kann mit Argumentieren oder Rechnen einsichtig gemacht werden.

 

Abb. 10: Kreisbšgen