Hans Walser, [20220218]

Flächengleichheit

1 Worum geht es?

Einfache Figur mit Flächengleichheit.

2 Flächengleiche Figuren

Das blaue Rechteck und das rote rechtwinklig gleichschenklige Dreieck sind flächengleich (Abb. 1).

Abb. 1: Rot = blau

Die Sache funktioniert auch für einen vollen Kreis (Abb. 2). Das blaue Rechteck und das rote Dreieck können sich überlappen.

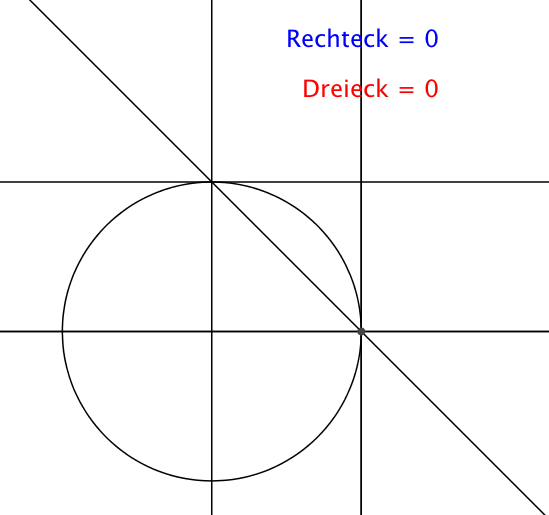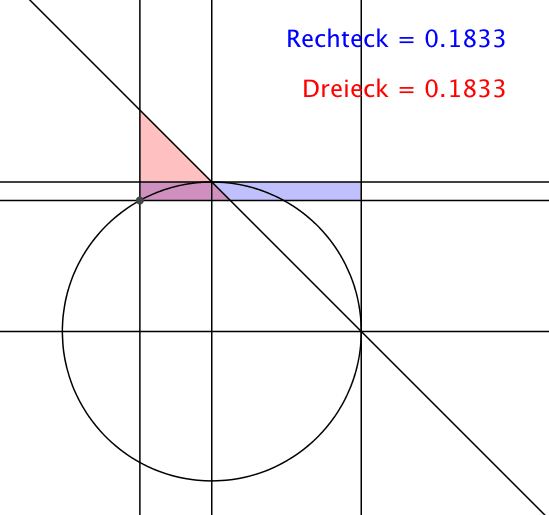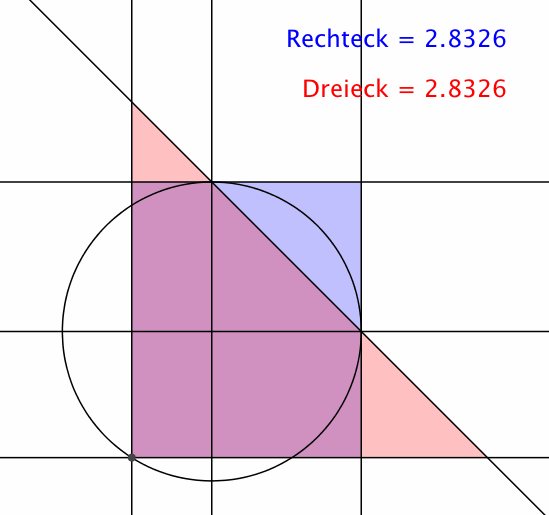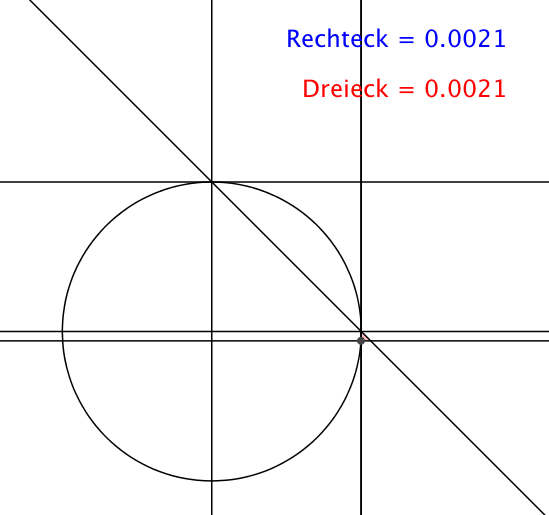
Abb. 2: Flächengleichheit

3 Rechnerische Beweise

3.1 Trigonometrie

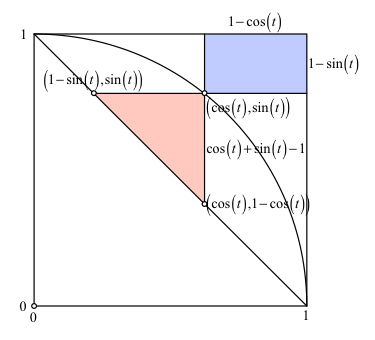
Abb. 3: Trigonometrischer Beweis

Wir interpretieren den Kreis als Einheitskreis und beschreiben den Schlüsselpunkt darauf mit:

(1)

Für den Flächeninhalt des blauen Rechteckes ergibt sich:

(2)

Das rote Dreieck hat die Kathetenlänge:

(3)

Daraus ergibt sich für den Flächeninhalt:

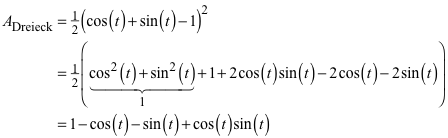(4)

Das Rechteck und das Dreieck haben also denselben Flächeninhalt.

3.2 Koordinatengeometrie

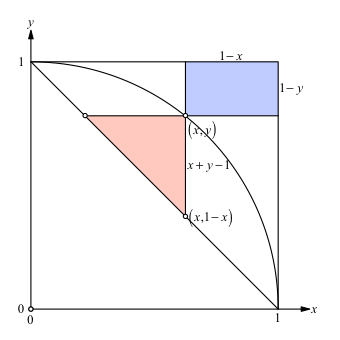
Abb. 4: Im Koordinatensystem

Wir interpretieren den Kreis als Einheitskreis:

(5)

Den Schlüsselpunkt beschreiben wir mit:

(6)

Für den Flächeninhalt des blauen Rechteckes ergibt sich:

(7)

Das rote Dreieck hat die Kathetenlänge:

(8)

Daraus ergibt sich für den Flächeninhalt:

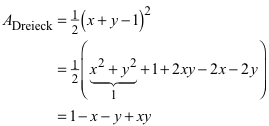(9)

Das Rechteck und das Dreieck haben denselben Flächeninhalt.

4 Zerlegungsgleichheit

Abb. 5: Gemeinsame Zerlegung

Die Abbildung 5 zeigt eine gemeinsame Zerlegung des Rechteckes und des Dreieckes.