Hans Walser, [20161016]

Flächenornamente

Anregung: Winkler (2016)

1 Worum geht es?

Es werden Flächenornamente als 2-reguläre Dreiecksfiguren dargestellt. Das sind Figuren, welche aus ausschließlich gleichseitigen kongruenten Dreiecken zusammengesetzt sind. Dabei kommen an jeder Dreiecksecke genau zwei Dreiecke zusammen.

2 Symmetrieklassen

Es gibt 17 Symmetrieklassen von Flächenornamenten (Fedorov 1891), (Pólya und Niggli 1942). Wir verwenden die Nummerierung nach Martin (1982) (Walser 2014, S. 84).

Zu jeder Symmetrieklasse wird ein Beispiel angegeben.

Eine analoge Klassifizierung der Bandornamente als 2-reguläre Dreiecksfiguren findet sich in [1].

2.1 Symmetrieklasse 1

2.2 Symmetrieklasse 2

2.3 Symmetrieklasse 3

2.4 Symmetrieklasse 4

2.5 Symmetrieklasse 5

2.6 Symmetrieklasse 6

2.7 Symmetrieklasse 7

2.8 Symmetrieklasse 8

2.9 Symmetrieklasse 9

2.10 Symmetrieklasse 10

2.11 Symmetrieklasse 11

2.12 Symmetrieklasse 12

2.13 Symmetrieklasse 13

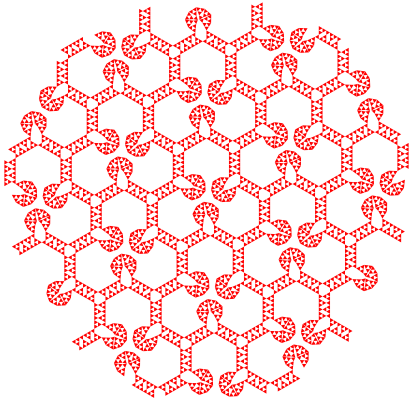
2.14 Symmetrieklasse 14

2.15 Symmetrieklasse 15

2.16 Symmetrieklasse 16

2.17 Symmetrieklasse 17

3 Klassifizierungsschema

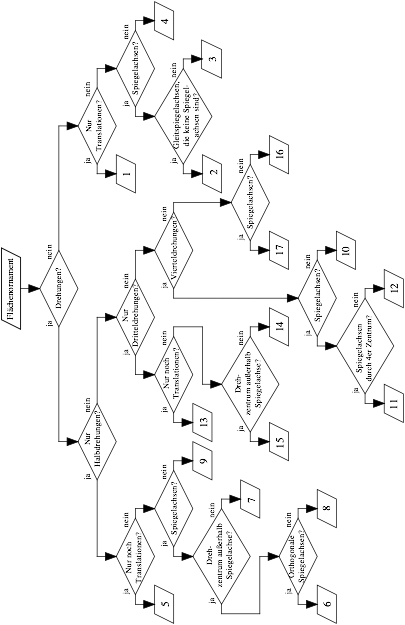
Literatur

Fedorov, E. S. (1891): Zapiski Mineralogicheskogo Imperatorskogo S. Petersburgskogo Obshchestva (2), 28, 345-390.

Martin, G. E. (1982): Transformation Geometry: An Introduction to Symmetry. New York: Springer. ISBN 0-387-90636-3.

Pólya, G. und Niggli, P. (1924): Zeitschrift für Kristallographie und Mineralogie, 60, 278-298.

Walser, Hans (2014): Symmetrie in Raum und Zeit. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-46-2.

Winkler, Mike (2016): Ein neuer 4-regulärer Streichholzgraph. Mitteilungen der DMV 24 / 2016. 74-75.

Winkler, Mike und Dinkelacker, Peter und Vogel, Stefan (2016): New minimal (4,n)-regular matchstick graphs. arXiv:1604.07134v2

Websites

[1] Hans Walser: Bandornamente (15.10.2016):

http://www.walser-h-m.ch/hans/Miniaturen/B/Bandornamente/Bandornamente.htm