Hans Walser, [20190512]
FlŠchensatz im Dreieck
1 Worum geht es?
Ein Satz źber Quadrate von FlŠchen im gleichseitigen Dreieck. Sonderfall einer Verallgemeinerung des Satzes von Pythagoras.
2 Der Satz
Auf dem Umkreis eines gleichseitigen Dreiecks ABC wŠhlen wir einen Punkt P wie zum Beispiel in der Abbildung 1.
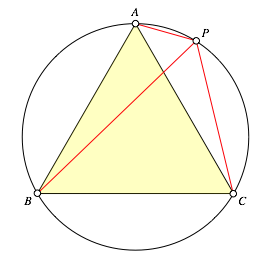
Abb. 1: Situation
Dann gilt (F bedeutet den FlŠcheninhalt):
![]() (1)
(1)
Wir haben es also mit einer Summe von Quadraten von FlŠchen zu tun. Die Sache spielt im vierdimensionalen Raum.
Formal ist es eine Verallgemeinerung des Satzes von Pythagoras. Wegen der VierdimensionalitŠt lassen sich die ăQuadrateŇ nicht durch geometrische Quadrate visualisieren.
3 Beweis
3.1 Bezeichnungen
Wir verwenden die Bezeichnungen der Abbildung 2.
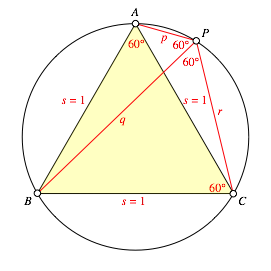
Abb. 2: Bezeichnungen
3.2 Normierung
Fźr die Rechnungen setzen wir die Dreiecksseite s = 1. Damit ist:
![]() (2)
(2)
3.3 Satz des PtolemŠus
Das Viereck ABCP ist ein Sehnenviereck. Nach dem Satz des PtolemŠus ist daher:
![]() (3)
(3)
3.4 Ohne Satz des PtolemŠus
Die
Beziehung (3) kann auch ohne den Satz des PtolemŠus hergeleitet werden. Dazu
unterteilen wir das Viereck ABCP in
zwei gleichseitige Dreiecke mit den SeitenlŠngen p und r (orange und
magenta in Abb. 3) sowie zwei kongruente und auch zum Dreieck PCA kongruente Dreiecke mit den
SeitenlŠngen p, r und s
(zyan und grźn). Darin kann die Beziehung (3) direkt abgelesen werden.
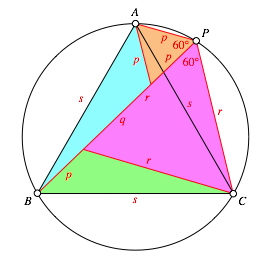
Abb.
3: Unterteilung
3.5 FlŠchenberechnungen
Der Umkreisbogen CA ist Ortsbogen fźr 60ˇ und 120ˇ. Wegen
![]() (4)
(4)
und (3) erhalten wir fźr die neuen DreiecksflŠchen:
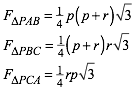 (5)
(5)
Mit (3), (4) und (5) erhalten wir fźr die linke Seite von (1) mit einiger Rechnung:
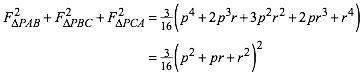 (6)
(6)
3.6 Kosinussatz
Aus dem Kosinussatz fźr das Dreieck PCA ergibt sich:
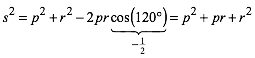 (7)
(7)
3.7 Schluss
Wegen s = 1 ist die letzte Klammer in (6) also 1. Damit hat die linke Seite von (1) denselben Wert wie die rechte Seite. Dies war zu zeigen.
Websites
Hans Walser: Verallgemeinerung des Satzes von Pythagoras
www.walser-h-m.ch/hans/Miniaturen/V/Verallg_Pythagoras2/Verallg_Pythagoras2.htm