1 Worum geht es?

Exemplarische Aufgabe im Umfeld des Flächenschwerpunktes eines Fünfeckes. „Schönes“ und unerwartetes Resultat.

2 Das Fünfeck

Wir setzen zwei Quadrate zu einem Rechteck zusammen (Abb. 1a). Auf dieses Rechteck setzen wir ein gleichseitiges Dreieck (Abb. 1b). So entsteht ein Fünfeck (Abb. 1c).

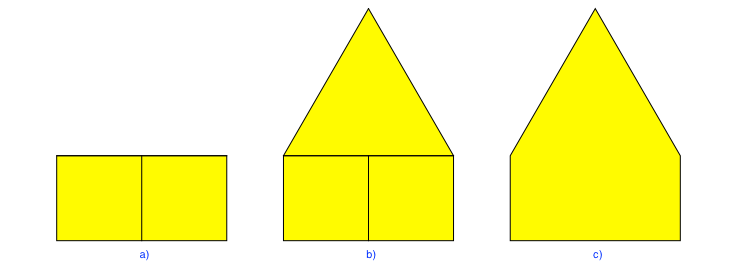
Abb. 1: Fünfeck

3 Problemstellung

Wo ist der Flächenschwerpunkt des Fünfeckes der Abbildung 1c?

4 Bearbeitung

Wir arbeiten im Koordinatensystem der Abbildung 2.

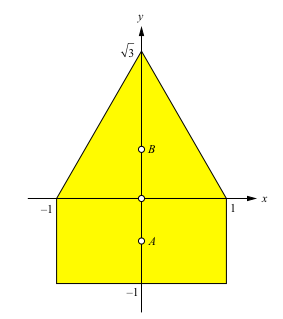
Abb. 2: Koordinatensystem

Aus Symmetriegründen liegt der Flächenschwerpunkt auf der y-Achse.

Der Flächenschwerpunkt A des aus den beiden Quadraten zusammengesetzten Rechteckes hat die Koordinaten A(0, –1/2). Das Rechteck hat den Flächeninhalt 2. Für das Drehmoment (Hebelarm mal Flächeninhalt) des Rechteckes gegenüber der x-Achse ergibt sich somit ½ • 2 = 1.

Das gleichseitige Dreieck hat den Flächenschwerpunkt B mit den Koordinaten B(0, √3/3) und den Flächeninhalt √3. Für das Drehmoment gegenüber der x-Achse ergibt sich √3/3 • √3 = 1.

Da die beiden Drehmomente gleich sind, liegt der gesuchte Flächenschwerpunkt auch auf der x-Achse.

Der gesuchte Flächenschwerpunkt ist also der Ursprung (0, 0) des Koordinatensystems und lässt sich leicht einzeichnen (Abb. 3).

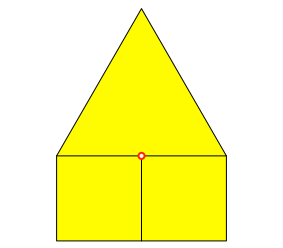
Abb. 3: Flächenschwerpunkt

5 Eckenschwerpunkt

Den Eckenschwerpunkt ergibt sich durch Ausmitteln der Koordinaten der Eckpunkte des Fünfeckes. Wir erhalten (0, 1/5 • (–2 + √3)) ≈ (0, –0.0536) (Abb. 4). Kein „schönes“ Resultat.

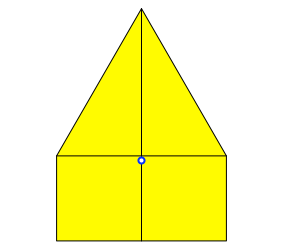
Abb. 4: Eckenschwerpunkt