1 Aufgabenstellung

Grünes Trapez ABCD in der üblichen Beschriftung.

Was hat es mit dem Punkt X auf sich (Abb. 1)?

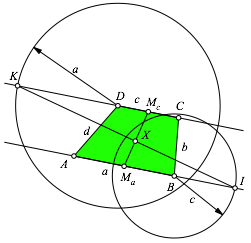
Abb. 1: Was ist mit dem Punkt X los?

2 Bearbeitung

Der Punkt X ist der Flächenschwerpunkt des Trapezes.

Man beachte, dass bei einem Viereck (allgemein bei einem Vieleck mit mehr als drei Ecken) der Flächenschwerpunkt in der Regel nicht der Eckenschwerpunkt ist. Das Ausmitteln der Eckpunktkoordinaten gibt den Eckenschwerpunkt, aber in der Regel nicht den Flächenschwerpunkt. Lediglich beim Dreieck fallen Flächenschwerpunkt und Eckenschwerpunkt immer zusammen.

2.1 Die schnelle Lösung

Bei GeoGebra gibt es den Befehl „Schwerpunkt(<Vieleck>)“. Er liefert den Flächenschwerpunkt.

2.2 Lege artis

Die ganze chose ist affin invariant. Das ist zunächst unglaubwürdig wegen der beiden Kreise, die natürlich nicht affin invariant sind. Sie dienen aber lediglich dazu, die Streckenlängen a beziehungsweise c auf dazu parallelen Geraden abzutragen. Das ist affin invariant.

Wir können die relevanten Teile der Figur also mit einer affinen Abbildung standardisieren gemäß Abbildung 2. Das Parallelogramm AICK wird auf das Einheitsquadrat abgebildet. Das hat den Vorteil, dass die Rechnungen etwas einfacher gehen.

Wir haben einen Parameter t im Spiel.

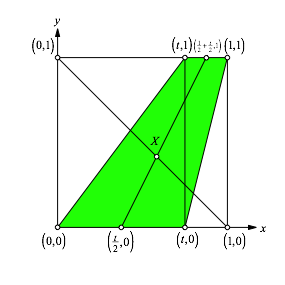
Abb. 2: Affine Standardisierung

Für X ergibt sich:

(1)

Wir müssen nun nachweisen, dass dies der Flächenschwerpunkt des grünen Trapezes ist. Wie gesagt, dürfen wir nicht einfach die Eckpunktkoordinaten ausmitteln (sonst wäre ja X auf halber Höhe, was offensichtlich nicht stimmt).

Die Berechnung des Flächenschwerpunktes geht in zwei Schritten (die beiden Schritte gestatten analog eine geometrische Konstruktion des Flächenschwerpunktes).

Erster Schritt: wir zerlegen das Trapez mit der senkrechten Diagonalen in zwei Dreiecke (Abb. 3).

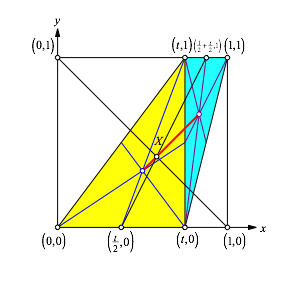
Abb. 3: Zerlegung in Dreiecke

In jedem der beiden Dreiecke berechnen wir den Dreieckschwerpunkt. Da wir bei Dreiecken die Eckpunktkoordinaten ausmitteln können, ist das dank der Standardisierung eine Kopfrechnung. Dann berechnen wir die Gerade durch die beiden Dreieckschwerpunkte (rot in Abb. 3). Der optische Befund zeigt, dass diese offenbar durch X verläuft. Das hat keine Beweiskraft, ist aber beruhigend.

Die rote Gerade ist übrigens parallel zur Quadratdiagonalen von links unten nach rechts oben. Dies ist eine Folge der Standardisierung.

Zweiter Schritt: wir wiederholen dasselbe Spielchen mit der andren Trapezdiagonalen (Abb. 4).

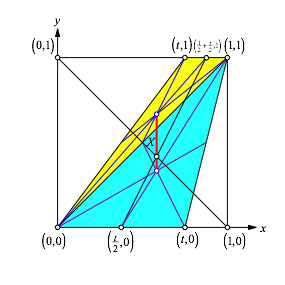
Abb. 4: Andere Zerlegung

Die rote Gerade ist jetzt senkrecht.

Nun schneiden wir die beiden roten Geraden und erhalten tatsächlich X gemäß (1).

Quod erat demonstrandum.

Literatur

Fritsch, Rudolf (2012): Zum Flächenschwerpunkt für Vierecke. Der mathematische und natur-wissenschaftliche Unterricht 65, 2012, S. 464–465.

Fritsch, Rudolf und Pickert, Günter (2014): Schwerpunkte von Vierecken. Die Wurzel, Heft 2 / 2014, 35-41.

Kirsch, A. (1987): Bemerkungen zum Vierecksschwerpunkt. Didaktik der Mathematik, 15, 34-36.

Kratz, Johannes (1994): „Das Schwerpunktsviereck“ – Eine Ergänzung zum Beitrag von Karl Seebach über Viereckschwerpunkte. Didaktik der Mathematik 22, 1994, S. 316–317.

Pickert, Günter (2013): Zu: Zum Flächenschwerpunkt für Vierecke. Der mathematische und naturwissenschaftliche Unterricht 66, 2013, Seiten 51–52.

Seebach, Karl (1983): Über Schwerpunkte von Dreiecken, Vierecken und Tetraedern, Teil 1. Didaktik der Mathematik 11, 1983, S. 270–282.

Seebach, Karl (1994): Nochmals: Viereckschwerpunkte. Didaktik der Mathematik 22, 1994, S. 309–315.

Walser, Hans (2012): Schwerpunkt. Mathematikinformation, 57, 14-22. ISSN 1612-9156.

Walser, Hans (2014): Flächenschwerpunkte. MNU, Der mathematische und naturwissenschaftliche Unterricht. 67. Dezember 2014, S. 466-467.

Weblinks

Thomas Jahre: Aufgabe der Woche

https://www.schulmodell.eu/aufgabe-der-woche.html

Thomas Jahre:

https://www.schulmodell.eu/unterricht/faecher/mathematik/wochenaufgabe/serie-55.html?start=8

Hans Walser: Schwerpunkte im Viereck

http://www.walser-h-m.ch/hans/Miniaturen/S/Schwerpunkte_Viereck/Schwerpunkte_Viereck.htm