Hans Walser, [20180726]
FlŠchenvergleich
Anregung: Muottas Muragl
1 Worum geht es?
FlŠchenvergleich im Quadratraster.
2 Die Figur
In ein 2×2-Quadratraster zeichnen wir vier gleichseitige Dreiecke gemŠ§ Abbildung 1a.
Den Rest fŠrben wir gemŠ§ Abbildung 1b.
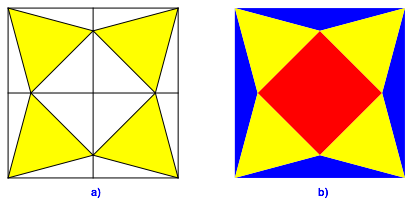
Abb. 1: Basisfigur. Rot = blau
Das rote Quadrat ist flŠchenmŠ§ig gleich der Summe der vier blauen Dreiecke.
3 Beweise
3.1 Rechnerischer Beweis
Wir setzen die RasterlŠnge 1.
Fźr das rote Quadrat erhalten wir:
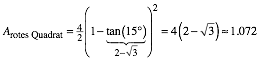 (1)
(1)
Das rote Quadrat ist also etwas grš§er als ein Rasterquadrat.
Fźr die Summe der vier blauen Dreiecke erhalten wir:
![]() (2)
(2)
3.2 Zerlegungsbeweis

Abb. 2: Zerlegungsbeweis
Der Zerlegungsbeweis enthŠlt SubtilitŠten. So ist etwa die lange Kathete des roten rechtwinkligen Dreieckes ein bisschen lŠnge als die halbe RasterlŠnge.
4 Parkett

Abb. 3: Rot = blau