Hans Walser, [20200112]

Flächenwinkel

Anfrage und Anregung: L. H., B.

1 Problemstellung

„Erläutern Sie Strategien zur Bestimmung von Flächenwinkeln bei halbregulären und regulären Polyedern“.

2 Vorbemerkungen

Der Flächenwinkel wird auch als Diederwinkel bezeichnet.

2.1 Symmetrien

Aus Symmetriegründen sind die meisten (oder sogar alle) Flächenwinkel gleich.

Reguläre und halbreguläre Polyeder haben fast immer einen Symmetriebezug zum Würfel.

2.2 Spezielle Lage

Spezielle Lage im Koordinatensystem: Mittelpunkt im Ursprung. Koordinatenebenen als Symmetrieebenen. Es müssen dann nur wenige Ecken koordinatenmäßig bestimmt werden, der Rest folgt aus der Symmetrie.

3 Standardverfahren

3.1 Normalvektoren

Der Schnittwinkel zweier Ebenen ist gleich dem Winkel zwischen den zugehörigen Normalvektoren. Mit Skalarprodukt berechenbar. Vorsicht: Oft ergibt sich der Außenwinkel des Polyeders.

Berechnung der Normalvektoren:

Ebene in Koordinatengleichung gegeben: Koeffizienten von x, y, z liefern einen Normalvektor.

Ebene in Parameterform gegeben: Das Crossproduct (Vektorprodukt) zweier Richtungsvektoren ist ein Normalvektor.

Sonderfall: Bei regulären und halbregulären Polyedern ist der Normalvektor einer Seitenfläche parallel zum arithmetischen Mittel der Vektoren vom Mittelpunkt des Polyeders zu den Eckpunkten der Seitenfläche. Dies aus Symmetriegründen.

3.2 Schnittebenen

Körper mit (Mittel-)Normalebene einer Kante schneiden. Der Winkel zwischen den Schnittgeraden ist der Flächenwinkel.

3.3 Spezielle Sicht

Polyeder so ansehen, dass zwei Seitenflächen mit gemeinsamer Kante nur noch als Strecken gesehen werden. Die gemeinsame Kante wird dann nur noch als Punkt gesehen. Der Winkel zwischen den Strecken ist der Flächenwinkel.

3.4 Sphärische Trigonometrie

Wir arbeiten mit einer Einheitskugel mit einer Polyederecke als Zentrum. Dort anschließende Seitenflächen schneiden ein (halb-)reguläres sphärisches Vieleck aus der Kugel. Die Innenwinkel der Seitenflächen des Polyeders sind die Seitenlängen des sphärischen Vielecks. Die Innenwinkel des sphärischen Vielecks sind die Flächenwinkel des Polyeders. Diese Innenwinkel sind mit sphärischer Trigonometrie berechenbar. Meist genügt der sphärische Seiten-Kosinus-Satz.

4 Komposition und Dekomposition

Beispiel: Wenn wir einem Oktaeder ein Tetraeder aufsetzen, ergibt sich eine durchgehende Ebene. Daher sind die Flächenwinkel von Oktaeder und Tetraeder Ergänzungswinkel auf 180°. Wenn der eine Flächenwinkel bekannt ist, kann der andere berechnet werden.

5 Beispiele

5.1 Kuboktaeder

Die Abbildung 1a zeigt ein dem blauen Würfel einbeschriebenes schwarzes Kuboktaeder. Der Koordinatenursprung ist im Mittelpunkt des Würfels und des Kuboktaeders. Auf den Achsen sind die Einheitspunkte angegeben. Das heißt, der Würfel hat die Kantenlänge 2.

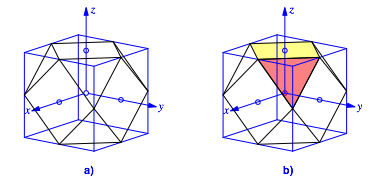
Abb. 1: Kuboktaeder

Aus der Abbildung 1a lassen sich die Eckpunktkoordinaten drei Eckpunkte mit nicht negativen Koordinaten ablesen. Die Koordinaten der übrigen neun Eckpunkte ergeben sich rein kombinatorisch durch geeignete Wahl der Vorzeichen:

(1)

Aus Symmetriegründen sind alle Flächenwinkel gleich groß. Wir berechnen den Flächenwinkel zwischen dem gelben Quadrat und dem roten Dreieck der Abbildung 1b.

5.1.1 Normalvektorenmethode

Das gelbe Quadrat hat den Normalvektor:

(2)

Das sehen wir einfach. Übungshalber berechnen wir es auch noch. Die Vektoren vom Mittelpunkt zu den vier Ecken des gelben Quadrates sind wegen (1):

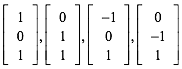(3)

Das arithmetische Mittel dieser vier Vektoren ist der Vektor (2).

Das rote Dreieck hat den Normalvektor:

(4)

Auch hier berechnen wir das übungshalber. Die drei Vektoren vom Mittelpunkt zu den drei Eckpunkten des roten Dreiecks sind:

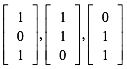(5)

Das arithmetische Mittel dieser drei Vektoren ist:

(6)

Dieser Vektor ist parallel zum Vektor (4).

Für die Winkelberechnung ist die Länge der Normalvektoren belanglos. Wir arbeiten daher mit den einfachsten Beispielen, also (2) und (4). Nach der Zwischenwinkelformel ist:

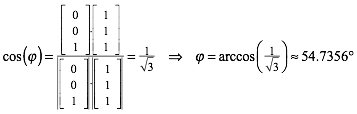(7)

Dies ist, als spitzer Winkel, der Außenwinkel. Für den Innenwinkel müssen wir auf 180° ergänzen und erhalten etwa 125.2644°.

5.1.2 Spezielle Sicht

Wir gucken das schwarze Kuboktaeder mitsamt dem blauen Würfel so an, dass wir das gelbe Quadrat und das rote Dreieck nur noch je als Strecke und die gemeinsame Kante dazwischen nur noch als Punkt sehen (Abb. 2).

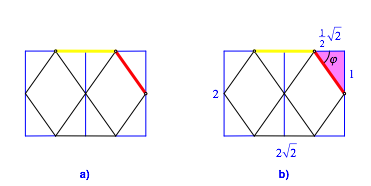
Abb. 2: Spezielle Sicht

Der Würfel erscheint jetzt in horizontaler Richtung mit dem Faktor auseinandergezogen. Das Kuboktaeder lässt sich problemlos einzeichnen.

Nun können wir mit dem Transporteur den Winkel zwischen der gelben und der roten Strecke (Abb. 2a) messen.

Oder wir können den Außenwinkel trigonometrisch gemäß Abbildung 2b berechnen. Im rosa eingezeichneten Dreieck ist:

(8)

Das hatten wir schon bei (7).

5.1.3 Ergänzungsmethode

Das Kuboktaeder kann hergestellt werden durch Abschneiden der Ecken von einem Oktaeder. Nun setzen wir umgekehrt eine solche Ecke wieder an, das heißt wir müssen eine Pyramide aufsetzen (Abb. 3a). Die Seitenflächen der Pyramide sind gleichseitige Dreiecke.

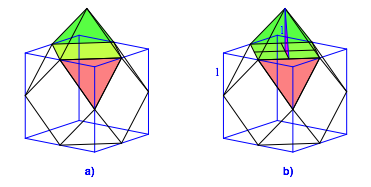
Abb. 3: Pyramide aufsetzen

Die vordere Seitenfläche der Pyramide liegt in einer Ebene mit dem roten Dreieck. Die Pyramide hat die Höhe 1 und die Kantenlänge . Damit lässt sich der Neigungswinkel einer Seitenfläche gegenüber dem Boden (also dem gelben Quadrat) berechnen. Als Hilfsmittel dient das in der Abbildung 3b eingezeichnete rosa Dreieck. Es ist rechtwinklig, hat eine Kathete 1 (die Pyramidenhöhe) und die andere Kathete . Es ist also dasselbe Dreieck wie das in der Abbildung 2b eingezeichnete rosa Dreieck. Somit erhalten wir wiederum den schon bekannten Außenwinkel.

Bemerkung 1: Die aufgesetzte Pyramide ist ein halbes Oktaederchen (Abb. 4a). Wenn der Flächenwinkel des Oktaeders bereits bekannt ist, erhalten wir durch Halbieren den Neigungswinkel gegenüber dem gelben Quadrat und damit den Außenwinkel des Kuboktaeders. Das ist die Methode „Ansetzen an Bekanntes“.

Bemerkung 2: Da wir jetzt den Außenwinkel schon kennen, erhalten wir durch Verdoppeln den Flächenwinkel des Oktaeders:

(9)

Dies ist der berühmte „kristallografische Winkel“. Er spielt in der Kristallografie eine wichtige Rolle. Der Ergänzungswinkel auf 180°, also der Winkel von etwa 70.5288°, ist der Flächenwinkel des Tetraeders. Dies wird sofort klar, wenn wir auf eine Seitenfläche des Oktaeders ein Tetraeder aufsetzen.

Bemerkung 3: Wenn wir in einem DIN A4-Papier die beiden Diagonalen einzeichnen, ergeben sich als Schnittwinkel der kristallografische Winkel und sein Ergänzungswinkel auf 180°, also die beiden Winkel von etwa 109.4712° und 70.5288° (Walser 2013).

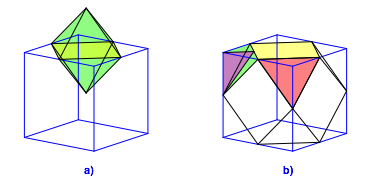
Abb. 4: Oktaederchen. Würfelecke

Bemerkung 4: Wer Lust hat, kann versuchen, statt der abgeschnittenen Oktaederecke eine abgeschnittene Würfelecke zu rekonstruieren (Abb. 4b). Wir erhalten wieder das rechtwinklige rosa Dreieck der Abbildungen 2b und 3b.

5.2 Tetraeder

Dies ist ein Beispiel zur Verwendung der sphärischen Trigonometrie.

Wir beginnen mit dem Tetraeder (Abb. 5.1).

Abb. 5.1: Tetraeder

An den Ecken des Tetraeders setzen wir blaue Kugeln mit dem Radius 1 an (Abb. 5.2).

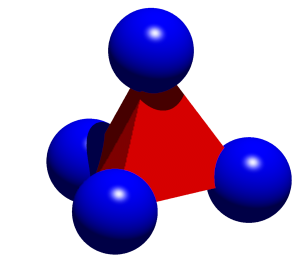
Abb. 5.2: Kugeln

Nun nehmen wir die Schnittfiguren des Tetraeders mit den Kugeln (Abb. 5.3).

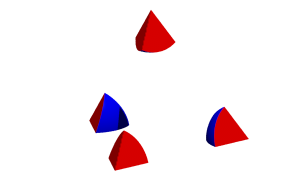
Abb. 5.3: Schnittfiguren

Wir erhalten blaue sphärische Dreiecke (Abb. 5.4). Die gleichseitigen Seitendreiecke des Tetraeders haben Winkel von 60° und ergeben daher für die blauen sphärischen Dreiecke eine Seitenlänge von . Dies ist das zu 60° gehörende Bogenmaß; die blauen Kugeln haben ja den Radius 1. Der in der Abbildung 5.4b eingezeichnete Winkel ist der gesuchte Flächenwinkel des Tetraeders. Dies ist darum so, weil die Kreisbögen der roten Sektoren rechtwinklig auf die Tetraederkanten auftreffen.

Abb. 5.4: Sphärisches Dreieck

Für die Berechnung von verwenden wir den sphärische Seiten-Kosinus-Satz. Dieser lautet allgemein in der üblichen Bezeichnung:

(10)

Auffallend ist, dass in der sphärischen Trigonometrie auch die Dreiecksseiten a, b, c als Inputs der Funktionen cos und sin erscheinen.

In unserem Fall ist . Wir erhalten also aus (10):

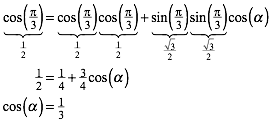(11)

Daraus ergibt sich:

(12)

6 Empirisches Vorgehen

Modell bauen. Winkel messen.

Der Modellbau gibt Hinweise auf die Berechnung der Flächenwinkel.

Die empirische Messung kann auch als Kontrolle der Rechnung dienen.

7 Warnungen

Es gibt keine schöne Formel für Flächenwinkel (Etwa in Analogie zur den Winkeln eines ebenen Vielecks, zum Beispiel dass die Summe der Innenwinkel des Dreiecks immer 180° ist).

Duale Körper haben nicht dieselben Flächenwinkel.

8 Sprachliches

Das Modewort „Strategie“ ist ein militärischer Ausdruck. Für die Mathematik nicht geeignet. Alternativen: „Methode“, „Verfahren“, „Vorgehensweise“, „Lösungsweg“

Websites

Hans Walser: Sphärische Trigonometrie

http://www.walser-h-m.ch/hans/Miniaturen/S/Sphaer_Trigo/Sphaer_Trigo.pdf

Hans Walser: Formeln für die sphärische, euklidische und hyperbolische Geoemtrie

http://www.walser-h-m.ch/hans/Miniaturen/F/Formeln/Formeln.htm

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.

Walser, Hans (2017): EAGLE STARTHILFE Kartografie. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-95922-098-9.

Walser, Hans (2018): Der Würfel. Ansichten – Dimensionen – Modelle. Edition am Gutenbergplatz, Leipzig 2018. ISBN 978-3-95922-102-3.