Hans Walser, [20200116]

Flächenwinkel bei regelmäßigen Polyedern

1 Worum geht es?

Einheitliche Formel zur Berechnung des Flächenwinkels bei regelmäßigen Polyedern. Herleitung mit sphärischer Trigonometrie.

2 Bezeichnungen

Die Seitenflächen des Polyeders sind regelmäßige n-Ecke.

An jeder Polyederecke kommen k Seitenflächen zusammen.

Beispiel Ikosaeder: n = 3, k = 5. An jeder Ecke kommen 5 Dreiecke zusammen.

3 Vorgehen

Wir schneiden eine Polyederecke mit einer Einheitskugel, welche ihr Zentrum in der Polyederecke hat.

3.1 Tetraeder

Wir illustrieren das Vorgehen zunächst am Tetraeder (Abb. 1.1).

Abb. 1.1: Tetraeder

An den Ecken des Tetraeders setzen wir blaue Kugeln mit dem Radius 1 an (Abb. 1.2). Es würde genügen, an einer einzigen Tetraederecke eine blaue Kugel anzusetzen,

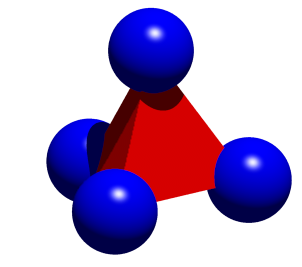
Abb. 1.2: Kugeln

Nun nehmen wir die Schnittfiguren des Tetraeders mit den Kugeln (Abb. 1.3).

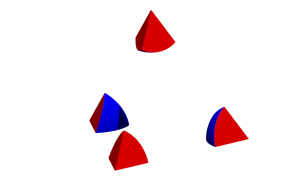
Abb. 1.3: Schnittfiguren

Wir erhalten blaue sphärische Dreiecke (Abb. 1.4). Die gleichseitigen Seitendreiecke des Tetraeders haben Winkel von 60° und ergeben daher für die blauen sphärischen Dreiecke eine Seitenlänge von . Dies ist das zu 60° gehörende Bogenmaß; die blauen Kugeln haben ja den Radius 1. Der in der Abbildung 1.4b eingezeichnete Winkel ist der gesuchte Flächenwinkel des Tetraeders. Dies ist darum so, weil die Kreisbögen der roten Sektoren rechtwinklig auf die Tetraederkanten auftreffen.

Abb. 1.4: Sphärisches Dreieck

3.2 Allgemein

Im allgemeinen Fall schneidet jede der k Seitenflächen des Polyeders aus der Kugel einen Sektor heraus. Das ergibt einen Kugelsektor (Abb. 2 für k = 5) und auf der Kugel ein regelmäßiges sphärisches k-Eck.

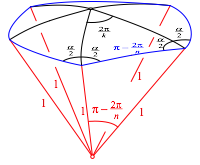
Abb. 2: Kugelsektor und regelmäßiges sphärisches k-Eck

Da die Seitenflächen des Polyeders regelmäßige n-Ecke sind, haben sie einen Innenwinkel . Dies ist auch die Seitenlänge des regelmäßigen sphärischen k-Ecks.

In der Abbildung 2 sind auch noch der Mittelpunkt des sphärischen k-Ecks und die Speichen eingezeichnet. Wegen der Regelmäßigkeit ergeben sich dort Winkel .

Die Abbildung 3a zeigt die Situation von oben.

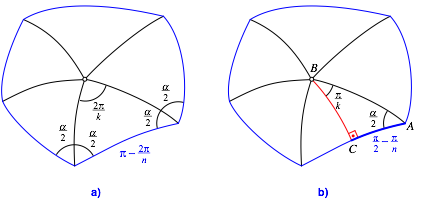
Abb. 3: Sicht von oben

Im Prinzip könnte man im einem der in der Abbildung 3a eingezeichneten Dreiecke mit dem Winkel-Kosinus-Satz weiterarbeiten. Es ist aber einfacher, den Symmetriebogen einzuzeichnen (Abb. 3b). So erhalten wir ein rechtwinkliges sphärisches Dreieck ABC.

Wir verwenden auch hier den Winkel-Kosinus-Satz. Dieser lautet allgemein:

(1)

In unserem Fall spielt die Rolle von . Weiter ist und . Schließlich ist . Damit erhalten wir aus (1):

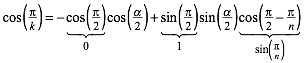(2)

Daraus ergibt sich die Superformel:

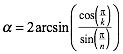(3)

4 Übersicht

Die Tabelle 1 gibt die numerischen Werte [°].

n	k	Flächenwinkel [°]	Bemerkung
3	2	0	Dreiecktüte
3	3	70.52877936	Tetraeder
3	4	109.4712206	Oktaeder
3	5	138.1896852	Ikosaeder
3	6	180	Dreiecksraster
3	7	180– 32.44409656i	komplex
4	2	0	Vierecktüte
4	3	90	Hexaeder (Würfel)
4	4	180	Quadratraster
4	5	180 – 60.80658181i	komplex
4	6	180 – 75.45612938i	komplex
4	7	180 – 83.02586576i	komplex
5	2	0	Fünfecktüte
5	3	116.5650511	Dodekaeder
5	4	180 – 71.83397196i	komplex
5	5	180 – 96.54133507i	komplex
5	6	180 – 107.5114763i	komplex
5	7	180 – 113.5852555i	komplex
6	2	0	Sechsecktüte
6	3	180	Bienenwabenmuster
6	4	180 – 100.9979734i	komplex
6	5	180 – 121.6131639i	komplex
6	6	180 – 131.3466595i	komplex
6	7	180 – 136.8457473i	komplex
7	2	0	Siebenecktüte
7	3	180 – 62.48389295i	komplex
7	4	180 – 122.6593618i	komplex
7	5	180 – 141.5196510i	komplex
7	6	180 – 150.6462673i	komplex
7	7	180 – 155.8504617i	komplex

Tab. 1: Flächenwinkel

Websites

Hans Walser: Flächenwinkel

http://www.walser-h-m.ch/hans/Miniaturen/F/Flaechenwinkel/Flaechenwinkel.htm

Hans Walser: Sphärische Trigonometrie

http://www.walser-h-m.ch/hans/Miniaturen/S/Sphaer_Trigo/Sphaer_Trigo.pdf

Hans Walser: Formeln für die sphärische, euklidische und hyperbolische Geometrie

http://www.walser-h-m.ch/hans/Miniaturen/F/Formeln/Formeln.htm

Literatur

Walser, Hans (2017): EAGLE STARTHILFE Kartografie. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-95922-098-9.