Hans Walser, [20191113]

FlŠchengleiche rechtwinklige Dreiecke

1     Worum geht es?

Wir bauen mit flŠchengleichen rechtwinkligen Dreiecken eine eckige Spirale.

2     Konstruktion

Wir beginnen mit einem rechtwinklig gleichschenkligen Dreieck der KathetenlŠnge 1 (Abb. 1b). Dieses Dreieck hat den FlŠcheninhalt . Dies soll auch der FlŠcheninhalt aller nachfolgenden Dreiecke sein.

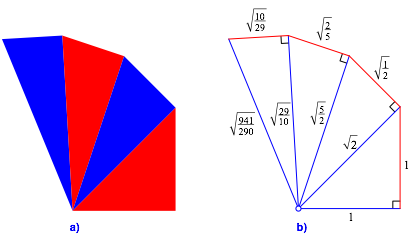
Abb. 1: Konstruktion

FŸr die Hypotenuse dieses ersten Dreiecks erhalten wir . Dies ist auch eine der beiden Katheten des zweiten Dreiecks. Aus der Bedingung der FlŠchengleichheit ergibt sich fŸr die andere Kathete des zweiten Dreiecks  und fŸr die Hypotenuse . Entsprechend fahren wir weiter. Die Abbildung 1a zeigt die ersten vier flŠchengleichen Dreiecke.

3     Berechnungen

3.1    Radikandenfolge

ZunŠchst berechnen wir die Radikandenfolge  fŸr die blauen Speichen. Diese kšnnen wir rekursiv berechnen. Wir setzen den Startwert

 

                                                                                                                             (1)

 

 

 

 

und arbeiten mit der Rekursion:

 

                                                                                                             (2)

 

 

 

 

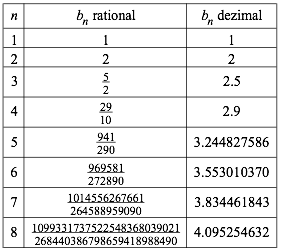
Die Tabelle 1 gibt die ersten 8 Werte der Folge (Abb. 1b).

 

                        

 

 

 

 

 

Tab. 1: Erste Werte

Die Folge wŠchst monoton, da immer etwas dazukommt. Die Frage ist, ob sie konvergiert oder divergiert.

3.2    Divergenz

Die Radikandenfolge  divergiert.

FŸr den Beweis der Divergenz vergleichen wir mit der Folge:

 

                                                                                                                  (3)

 

 

 

Die Tabelle 2 gibt die ersten numerischen Werte.

 

n

1

1

1.414213562

–0.414213562

2

2

2

0

3

2.5

2.449489743

0.050510257

4

2.9

2.828427124

0.071572876

5

3.244827586

3.162277660

0.082549926

6

3.553010370

3.464101616

0.088908754

7

3.834461842

3.741657387

0.092804455

8

4.095254632

4

0.095254632

9

4.339439692

4.242640686

0.096799006

10

4.569884190

4.472135954

0.097748236

11

4.788708116

4.690415760

0.098292356

12

4.997532704

4.898979486

0.098553218

13

5.197631445

5.099019514

0.098611931

14

5.390026772

5.291502622

0.098524150

15

5.575554607

5.477225575

0.098329032

16

5.754908962

5.656854248

0.098054714

17

5.928673657

5.830951895

0.097721762

18

6.097345447

6

0.097345447

19

6.261351244

6.164414003

0.096937241

20

6.421061179

6.324555320

0.096505859

Tab. 2: Vergleich der beiden Folgen

FŸr  ist . Dies kann induktiv gezeigt werden. Wir arbeiten mit der Funktion:

 

                                                                                                              (4)

 

 

 

Der Funktionsgraf ist durchgehend negativ gekrŸmmt (Abb. 2). FŸr die erste Ableitung erhalten wir:

 

                                                                               (5)

 

 

 

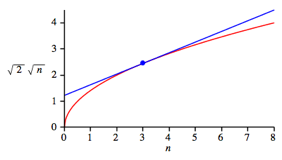
Abb. 2: AbschŠtzung

Nach Newton ist exemplarisch fŸr n = 3:

 

                                                                       (6)

 

 

 

Wegen der negativen KrŸmmung des Funktionsgrafen kann eine einseitige AbschŠtzung gemacht werden:

 

                                                                       (7)

 

 

 

Allgemein ist:

 

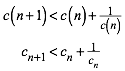                                                                                                (8)

 

 

 

 

 

 

Vergleich mit (2) zeigt, dass die Folge  fŸr  eine Minorante der Folge  ist. Da die Folge   divergiert, tut dies auch die Folge .

3.3    Speichen und Winkel

FŸr die vom Zentrum ausgehenden Speichen  gilt:

 

                                                                                                                     (9)

 

 

 

Die Speichenfolge  divergiert ebenfalls. FŸr die Dreieckswinkel  beim Zentrum gilt:

 

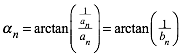                                                                           (10)

 

 

 

 

Damit haben wir ausreichend Informationen, um die Dreiecksfolge zu zeichnen.

4     Beispiele

Die Abbildung 3 zeigt die ersten 30 Dreiecke.

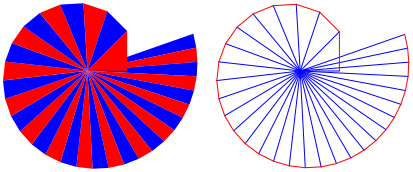
Abb. 3: Die ersten 30 Dreiecke

Die Abbildung 4 zeigt die ersten 1000 Dreiecke.

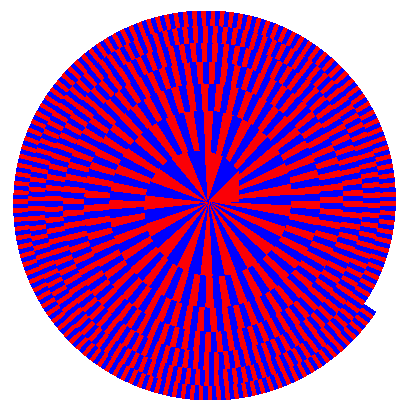
Abb. 4a: Die ersten 1000 Dreiecke

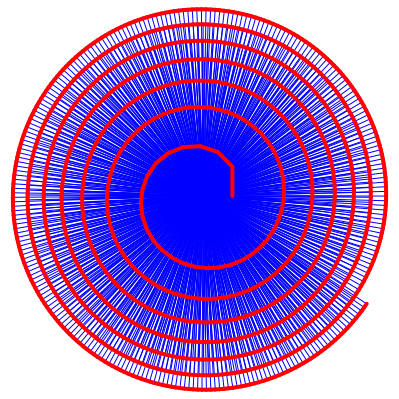
Abb. 4b: Die ersten 1000 Dreiecke

5     Approximation

Die rote eckige Spirale kann approximiert werden durch die Spirale (grŸn in Abb. 5) mit der Polardarstellung:

 

                                                                                                         (11)

 

 

 

Abb. 5: Approximation