Hans Walser, [20160428]
Flossen
1 Worum es geht
Nach Ansetzen von Quadraten an ein Polygon ergeben sich Zwischenfiguren (Dreiecke oder Vierecke, ãFlossenÒ). Bei beliebigen Dreiecken, beliebigen Vierecken und punktsymmetrischen Sechsecken ergeben sich ganzzahlige Flchenverhltnisse. Die Zahlen sind mit den Fibonacci-Zahlen verwandt.
Beweise fehlen.
2 Dreieck als Basis
Einem Dreieck setzen wir Quadrate an und fllen die Zwischenrume mit roten Dreiecken (Abb. 1) (vgl. [1], [2] ).

Abb. 1: Dreieck als Basis. Erste Runde
Anschlie§end setzen wir den roten Au§enkanten Quadrate an und fllen die Zwischenrume mit roten blauen Vierecken (Abb. 2). So erhalten wir die zweite Runde.
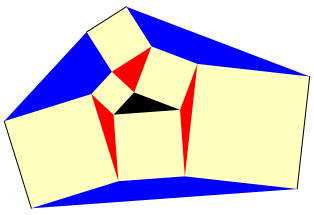
Abb. 2: Zweite Runde (blau)
Nun fahren wir entsprechend weiter und erhalten die dritte Runde (grn in Abb. 3).

Abb. 3: Dritte Runde grn
Und noch die vierte Runde (Abb. 4).
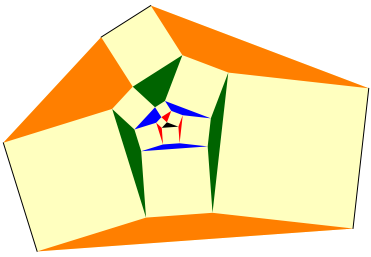
Abb. 4: Vierte Runde orange
Nun gilt folgendes.
Die Dreiecke und Vierecke gleicher Farbe sind flchenm§ig je gleich gro§.
In der Tabelle 1 werden die Flchenverhltnisse der drei Figuren einer Farbe im Verhltnis zum Flcheninhalt des schwarzen Ausgangsdreieckes aufgelistet. Der Flcheninhalt des schwarzen Ausgangsdreieckes ist also die Ma§einheit fr die Flchenmessung.
|
Nummer |
1 |
2 |
3 |
4 |
|
Farbe |
rot |
blau |
grn |
orange |
|
Flche |
3 |
15 |
72 |
345 |
Tab. 1: Flchenverhltnisse
Fr die Folge fn der Flchen gilt die Rekursion
![]() (1)
(1)
und die explizite Formel:
![]() (2)
(2)
Die Tabelle 2 gibt die ersten 20 Werte von fn. Vgl. https://oeis.org/A004254 und [5]. Wegen (2) wachsen die Werte im Wesentlichen exponentiell.
|
n |
fn |
|
n |
fn |
|
1 |
3 |
|
11 |
19997997 |
|
2 |
15 |
|
12 |
95816160 |
|
3 |
72 |
|
13 |
459082803 |
|
4 |
345 |
|
14 |
2199597855 |
|
5 |
1653 |
|
15 |
10538906472 |
|
6 |
7920 |
|
16 |
50494934505 |
|
7 |
37947 |
|
17 |
241935766053 |
|
8 |
181815 |
|
18 |
1159183895760 |
|
9 |
871128 |
|
19 |
5553983712747 |
|
10 |
4173825 |
|
20 |
26610734667975 |
Tab. 2: Werte
Mit den Koeffizienten der Rekursionsformel (1) basteln wir ein Polynom:
![]() (3)
(3)
Nun machen wir eine Taylor-Entwicklung des Terms
![]() (4)
(4)
an der Stelle x = 0 und erhalten:
![]() (5)
(5)
Die Koeffizienten sind die Werte unserer Folge.
3 Viereck als Basis
Die Abbildung 5 zeigt die analoge Figur mit einem beliebigen Viereck als Startfigur.
Im Unterschied zum Dreiecksfall sind die Vielecke gleicher Farbe nicht mehr flchengleich.
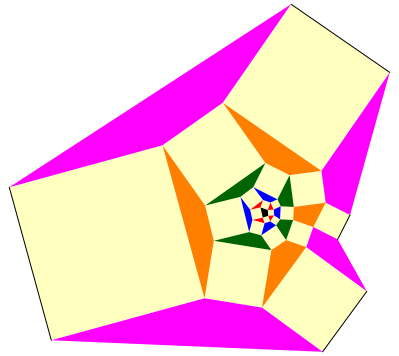
Abb. 5: Viereck als Startfigur
In der Tabelle 3 werden die Flchenverhltnisse der vier Figuren einer Farbe im Verhltnis zum Flcheninhalt des schwarzen Ausgangsviereckes aufgelistet. Der Flcheninhalt des schwarzen Ausgangsviereckes ist also die Ma§einheit fr die Flchenmessung.
|
Nummer |
1 |
2 |
3 |
4 |
5 |
|
Farbe |
rot |
blau |
grn |
orange |
magenta |
|
Flche |
2 |
8 |
30 |
112 |
418 |
Tab. 3: Flchenverhltnisse
Fr die Folge fn der Flchen gilt die Rekursion
![]() (6)
(6)
und die explizite Formel:
![]() (7)
(7)
Die Tabelle 4 gibt die ersten 20 Werte von fn. Vgl. https://oeis.org/A052530. Wegen (7) wachsen die Werte im Wesentlichen exponentiell.
|
n |
fn |
|
n |
fn |
|
1 |
2 |
|
11 |
1129438 |
|
2 |
8 |
|
12 |
4215120 |
|
3 |
30 |
|
13 |
15731042 |
|
4 |
112 |
|
14 |
58709048 |
|
5 |
418 |
|
15 |
219105150 |
|
6 |
1560 |
|
16 |
817711552 |
|
7 |
5822 |
|
17 |
3051741058 |
|
8 |
21728 |
|
18 |
11389252680 |
|
9 |
81090 |
|
19 |
42505269662 |
|
10 |
302632 |
|
20 |
158631825968 |
Tab. 4: Werte
Taylor:
![]() (8)
(8)
Fr den Sonderfall eines Parallelogramms vergleiche [3].
4 Punktsymmetrisches Sechseck als Basis
Die Abbildung 6 zeigt die analoge Figur mit einem beliebigen punktsymmetrischen Sechseck als Startfigur (vgl. [4]).
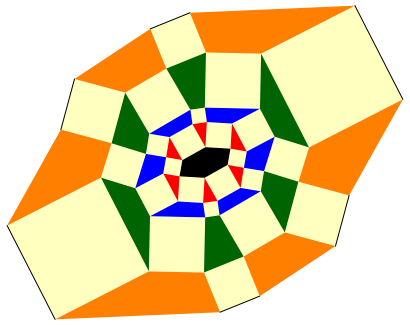
Abb. 6: Punktsymmetrisches Sechseck als Startfigur
In der Tabelle 5 werden die Flchenverhltnisse der sechs Figuren einer Farbe im Verhltnis zum Flcheninhalt des schwarzen Ausgangssechseckes aufgelistet..
|
Nummer |
1 |
2 |
3 |
4 |
|
Farbe |
rot |
blau |
grn |
orange |
|
Flche |
1 |
3 |
8 |
21 |
Tab. 5: Flchenverhltnisse
Fr die Folge fn der Flchen gilt die Rekursion
![]() (9)
(9)
und die explizite Formel:
![]() (9)
(9)
Die Tabelle 4 gibt die ersten 20 Werte von fn. Es handelt sich um jedes zweite Folgenglied der Fibonacci-Folge (Walser 2012). Wer htte das gedacht.
|
n |
fn |
|
n |
fn |
|
1 |
1 |
|
11 |
17711 |
|
2 |
3 |
|
12 |
46368 |
|
3 |
8 |
|
13 |
121393 |
|
4 |
21 |
|
14 |
317811 |
|
5 |
55 |
|
15 |
832040 |
|
6 |
144 |
|
16 |
2178309 |
|
7 |
377 |
|
17 |
5702887 |
|
8 |
987 |
|
18 |
14930352 |
|
9 |
2584 |
|
19 |
39088169 |
|
10 |
6765 |
|
20 |
102334155 |
Tab. 6: Fibonacci-Auswahl
Taylor:
![]() (10)
(10)
Literatur
Deshpande, M. N. (2009): Proof Without Words: Beyond Extriangles. MATHEMATICS MAGAZINE. Vol. 82, No. 3, June 2009, p. 208.
Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.
Websites
Abgerufen 27. April 2016
[1] http://www.walser-h-m.ch/hans/Miniaturen/P/Puzzle_2/Puzzle_2.htm
[2] http://www.walser-h-m.ch/hans/Miniaturen/P/Puzzle_4/Puzzle_4.htm
[3] http://www.walser-h-m.ch/hans/Miniaturen/P/Puzzle/Puzzle.htm
[4] http://www.walser-h-m.ch/hans/Miniaturen/P/Puzzle_3/Puzzle_3.htm
[5] https://oeis.org