1 Worum es geht

Wir bearbeiten Folgen a_n mit dem Startwert a₀ und der Rekursion:

(1)

Es handelt sich also um eine Mischform von geometrischer und arithmetischer Folge.

2 Explizite Form

Es ist:

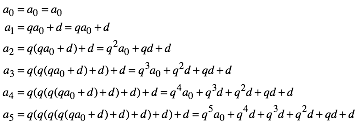(2)

Allgemein ist für :

(3)

Durch Umformen ergibt sich:

(4)

Es handelt sich also im Wesentlichen um eine geometrische Folge.

3 Summenfolge

Wir berechnen die Summenfolge s_n:

(5)

Es ist:

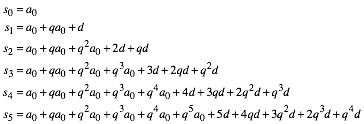(6)

Allgemein:

(7)

Umformen ergibt:

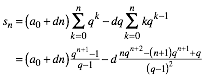(8)

4 Numerische Beispiele

Für a₀ = 1, f = 2 und d = 1 ergeben sich die Werte der Tabelle 1.

n	a_n	s_n
0	1	1
1	3	4
2	7	11
3	15	26
4	31	57
5	63	120

Tab. 1

Für a₀ = 1, f = 2 und d = 0 ergeben sich die Werte der Tabelle 2.

n	a_n	s_n
0	1	1
1	2	3
2	4	7
3	8	15
4	16	31
5	32	63

Tab. 2

Für a₀ = 1, f = 1 und d = 1 ergeben sich die Werte der Tabelle 3.

n	a_n	s_n
0	1	1
1	2	3
2	3	6
3	4	10
4	5	15
5	6	21

Tab. 3

Für a₀ = 1, f = 0.9 und d = 0.1 ergeben sich die Werte der Tabelle 4. Die Folge a_n ist konstant.

n	a_n	s_n
0	1	1
1	1.0	2.0
2	1.00	3.00
3	1.000	4.000
4	1.0000	5.0000
5	1.00000	6.00000

Tab. 4

Für a₀ = 1, f = 9/10 und d = 1/10 ergeben sich die Werte der Tabelle 5. Die Folge a_n ist konstant. Der Unterschied zu den Werten der Tabelle 4 ergibt sich durch eine unterschiedliche Rechenart (Brüche statt Dezimalzahlen)

n	a_n	s_n
0	1	1
1	1	2
2	1	3
3	1	4
4	1	5
5	1	6

Tab. 5

Bei anderen Startwerten steigt oder fällt die Folge.

Für a₀ = 0.5, f = 0.9 und d = 0.1 ergeben sich die Werte der Tabelle 6. Die Folge a_n steigt, hat aber die Obergrenze 1.

n	a_n	s_n
0	0.5	0.5
1	0.55	1.05
2	0.595	1.645
3	0.6355	2.2805
4	0.67195	2.95245
5	0.704755	3.657205

Tab. 6

Für a₀ = 1.5, f = 0.9 und d = 0.1 ergeben sich die Werte der Tabelle 7. Die Folge a_n fällt, hat aber die Untergrenze 1.

n	a_n	s_n
0	1.5	1.5
1	1.45	2.95
2	1.405	4.355
3	1.3645	5.7195
4	1.32805	7.04755
5	1.295245	8.342795

Tab. 7