Hans Walser, [20090207a]

Folgen im Schachbrett

1        Harmonische Folgen

1.1      Konstruktion

Wir beginnen mit Gitterpunkten im Schachbrett und zeichnen eine Zickzack-Linie, deren Ecken zu harmonischen Folgen fźhren.

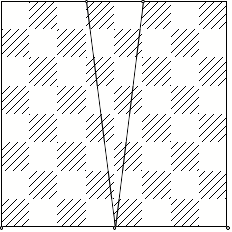
Start

Die folgende Figur zeigt den ersten Schritt der Konstruktion der Zickzack-Linie.

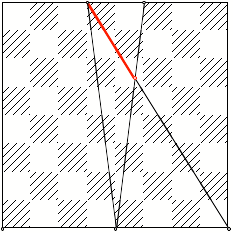
Erster Schritt

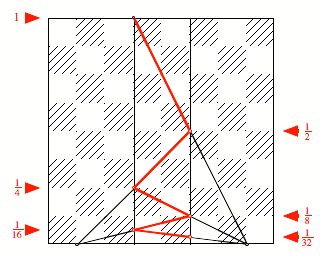
Nun folgen weitere Schritte. An den RŠndern sind die relativen Hšhen der Eckpunkte der Zickzack-Linie im Vergleich zur SeitenlŠnge des Schachbrettes vermerkt. Diese Hšhen lassen sich mit einem geeigneten Koordinatensystem berechnen.

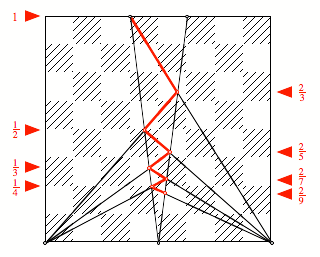
Weitere Schritte

Am linken Rand erkennen wir die klassische harmonische Folge . Der Beweis lŠsst sich induktiv fźhren.

Was hat es mit den Zahlen am rechten Rand auf sich?

1.2      Das harmonische Mittel

Unter dem harmonischen Mittel h zweier Zahlen a und b verstehen wir:

Beispiel: Ein Autorennfahrer fŠhrt die erste Runde (der LŠnge s) mit der Geschwindigkeit  und die zweite Runde mit der Geschwindigkeit . Wie gro§ ist die Durchschnittsgeschwindigkeit in diesen ersten beiden Runden zusammen?

Bearbeitung: Fźr die erste Runde ist ein Zeitaufwand  erforderlich, entsprechend fźr die zweite Runde . Die Durchschnittsgeschwindigkeit  ist also:

Wir erhalten das harmonische Mittel der beiden einzelnen Geschwindigkeiten. Die LŠnge s des Rennringes spielt keine Rolle.

1.3      Harmonische Folgen

In der klassischen harmonischen Folge  ist jedes Folgenglied das harmonische Mittel der beiden Nachbarglieder. Wir reden nun allgemein von einer harmonischen Folge , wenn . Unter diesem Aspekt bilden auch die Zahlen  am rechten Rand eine harmonische Folge, ebenso die Folge, dies sich aus der Vereinigung der beiden Folgen ergibt:

Aus der Definitionsbedingung  ergibt sich die Rekursionsformel:

Wegen dem Minuszeichen im Nenner kann es zu einer Division durch Null kommen. Bei den Startwerten  und  etwa muss man mit Gefźhl arbeiten:

Bei den Startwerten  und  tritt der Pol nicht auf:


2        Geometrische Folgen

2.1      Konstruktion

Wir beginnen mit Gitterpunkten im Schachbrett und zeichnen eine Zickzack-Linie, deren Ecken zu geometrischen Folgen fźhren.

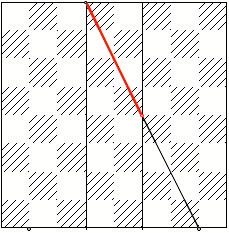
Erster Schritt

Weitere Schritte

Es entsteht eine geometrische Folge. Der Beweis ergibt sich aus den StrahlensŠtzen.