Hans Walser, [20091025c]
Variationen zu Ford-Kreisen
Inhalt
1 Die
Ford-Kreise........................................................................................................... 1
2 Kreise
oben.................................................................................................................. 2
3 Vierteilige
Symmetrie.................................................................................................. 4
4 Dreiteilige
Symmetrie.................................................................................................. 6
5 Rechentechnisches....................................................................................................... 6
1 Die Ford-Kreise
Unter den Ford-Kreisen
versteht man die Kreise der folgenden Figur.
Ford-Kreise
Wir vereinfachen die
Figur.
Vereinfachung
Wir verwenden ein
Koordinatensystem.
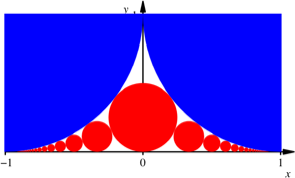
Koordinatensystem
Die blauen
Viertelkreise haben in diesem Koordinatensystem die Radien 1. Der zentrale rote
Kreis hat den Radius 
, die anschlie§enden Kreise der Reihe nach die Radien 
, 
, 
, ..., allgemein:
.
2 Kreise oben
Nun fźllen wir oberhalb
des zentralen roten Kreises mit weiteren Kreisen.
Weitere Kreise
Fźr die Radien der
roten Kreise gilt:
r[0] = 1/4
r[1] = 1/12
r[2] = 1/24
r[3] = 1/40
r[4] = 1/60
r[5] = 1/84
r[6] = 1/112
r[7] = 1/144
r[8] = 1/180
r[9] = 1/220
r[10] = 1/264
Die Radien sind
Kehrwerte einer arithmetischen Folge zweiter Ordnung:
Der €sthetik halber
noch die †berlagerung.
†berlagerung
SŠmtliche Radien der
roten Kreise sind rational.
3
Vierteilige Symmetrie
Vierteilige Symmetrie
Hier sind die Radien
der roten Kreise nicht mehr rational, schon der zentrale rote Kreis hat den
Radius 
.
Fźr die Radien erhalten
wir der Reihe nach:
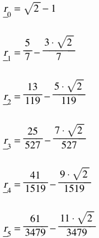
Allgemein gilt:
4
Dreiteilige Symmetrie
Dreiteilige Symmetrie
Fźr die Radien gilt:
5
Rechentechnisches
Die Berechnung der
Radien erfolgte rekursiv unter Verwendung des Satzes von Pythagoras. Berechnung
mit CAS (MuPAD).