1 Worum es geht

Radienberechnung. Satz des Pythagoras. Rationale Lösungen. Pythagoreische Dreiecke.

2 Die klassische Schulaufgabe

Eine klassische Schulaufgabe besteht darin, den Radius des roten Füllkreises (Abb. 1) zu berechnen.

Abb. 1: Füllkreis

Die Aufgabe kann mit dem Satz des Pythagoras gelöst werden.

Wir setzen die Quadratseite auf 1. Gesucht ist der Kreisradius r₁ des roten Kreises.

Abb. 2: Bearbeitung

Im roten rechtwinkligen Dreieck (Abb. 2) ist die Hypotenuse 1 – r₁, die kurze Kathete r₁ und die lange Kathete ½. Gemäß dem Satz des Pythagoras ist.

(1 – r₁)² = r₁² + (½)²

Der Witz der Sache ist nun, dass bei der Vereinfachung dieser Gleichung der Quadratische Term r₁² „herausfällt“ und eine lineare Gleichung mit einer rationalen Lösung übrigbleibt:

1 – 2r₁ = ¼

r₁ = ⅜

3 Pythagoreisches Dreieck

Das rote rechtwinklige Dreieck hat die Seiten ⅜, ½ und ⅝. Es hat also das Seitenverhältnis 3:4:5 und ist damit ein pythagoreisches Dreieck.

4 Weitere Füllkreise

In der Abbildung 3 ist ein zweiter Füllkreis eingezeichnet.

Abb. 3: Zweiter Füllkreis

Für seinen Radius r₂ arbeiten wir mit dem magenta rechtwinkligen Dreieck (Abb. 4). Es hat die Hypotenuse 1 + r₂, die längere Kathete 1 – r₂ und die kürzere Kathete ½.

Der Satz des Pythagoras liefert wiederum eine lineare Gleichung mit der rationalen Lösung:

r₂ = 1/16

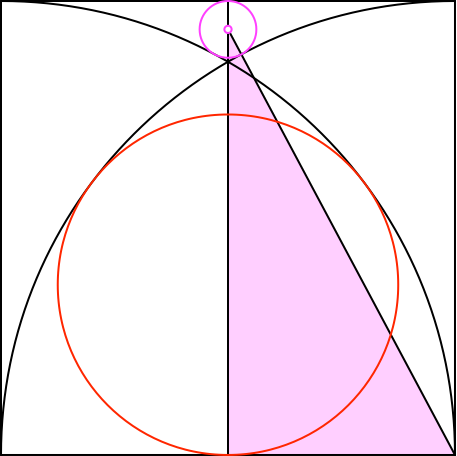
Abb. 4: Bearbeitung

Das magenta rechtwinklige Dreieck hat die Seiten 17/16, 15/16, ½. Es hat also das Seitenverhältnis 15:8:17 und ist damit ebenfalls ein pythagoreisches Dreieck.

Aus den berechneten Radien für den roten und den magenta Füllkreis folgt, dass wir einen weiteren magenta Kreis exakt dazwischen einpassen können (Abb. 5). Dieser Kreis ist aber kein Füllkreis.

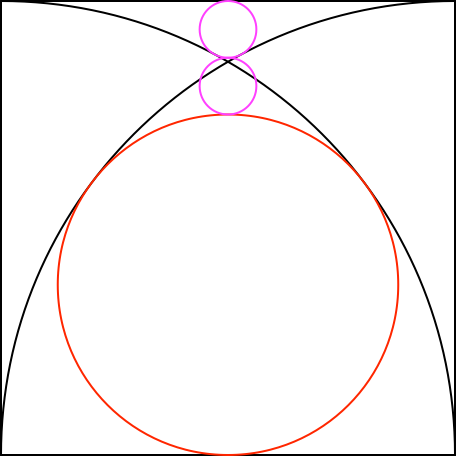
Abb. 5: Drei Kreise

Wir können noch zwei weitere, blaue Füllkreise einfügen (Abb. 6).

Abb. 6: Weitere Füllkreise

Für die Berechnung des Radius r₃ der blauen Füllkreise arbeiten wir mit zwei rechtwinkligen Dreiecken (Abb. 7).

Abb. 7: Zwei rechtwinklige Dreiecke

Die beiden Dreiecke haben eine Kathete gemeinsam. Daher ist:

(1 + r₃)² – (1 – r₃)² = (1 – r₃)² – r₃²

Es fällt vieles heraus und wir erhalten die rationale Lösung:

r₃ = ⅙

Die gemeinsame Kathete der beiden rechtwinkligen Dreiecken in der Abbildung 7 hat die irrationale Länge √(⅔) ≈ 0.816. Die beiden Dreiecke sind daher nicht pythagoreisch.

Durch Einfügen zweier Kreissektoren (gelb in Abb. 8) und eines dritten blauen Kreises gewinnen wir aber die Anhaltspunkte für ein pythagoreisches Dreieck (hellblau in Abb. 8). Es hat die Seiten ½, ⅔ und ⅚, also das Seitenverhältnis 3:4:5.

Abb. 8: Pythagoreisches Dreieck

Statt mit zwei Kreissektoren können wir auch mit einem Halbkreis arbeiten (Abb. 9). Der dritte blaue Kreis ist dann ebenfalls ein Füllkreis.

Abb. 9: Halbkreis

Wegen r₃ = ⅙ können wir einen weiteren blauen Kreis exakt zwischen die beiden blauen Füllkreise einpassen (Abb. 10). Dieser ist kein Füllkreis mehr.

Abb. 10: Weiterer blauer Kreis