Hans Walser, [20091125a]
Fźnf-Punkte-Kreise
1 Einstiegsbeispiel
Wir
drehen eine Gerade 
um einen nicht
auf dieser Geraden liegenden Punkt 
um die Winkel 
, 
und 
mit beliebigem
Winkel 
. Die Bildgeraden hei§en 
, 
und 
.
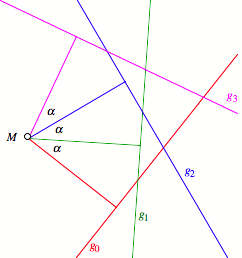
Verdrehte
Geraden
Nun gibt
es einen Kreis, der durch vier Schnittpunkte dieser Geraden sowie durch 
verlŠuft.
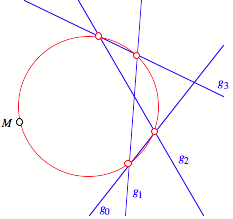
Fźnf-Punkte-Kreis
2
Beweis
Bezeichnungen
gemŠ§ Figur.
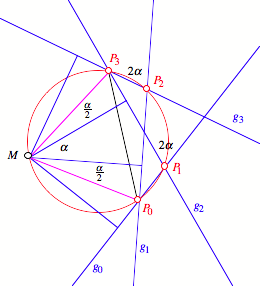
Beweisfigur
GemŠ§
Konstruktion schneiden sich die Geraden 
und 
unter dem Winkel
, dasselbe tun die Geraden 
und 
. Die Schnittpunkte 
beziehungsweise 
liegen also auf
dem Fasskreis źber der Strecke 
fźr den
Peripheriewinkel 
. Wegen 
liegt auch der
Punkt 
auf diesem
Kreis.
3
Verallgemeinerung
Die in
der Figur dargestellten Verallgemeinerungen lassen sich analog beweisen.
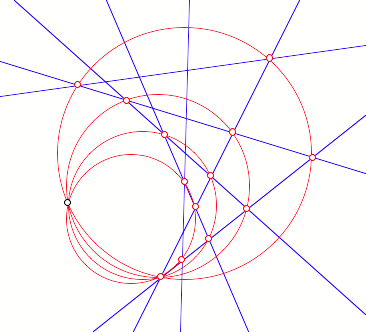
Verallgemeinerung
4
SonderfŠlle und Bildergalerie
Die
TrŠgergeraden eines regelmŠ§igen Vieleckes erfźllen die Voraussetzungen unserer
†berlegungen, daher gibt es entsprechende Fźnf-Punkte-Kreise.
Im
Folgenden einige Beispiele.
4.1
RegelmŠ§iges Fźnfeck
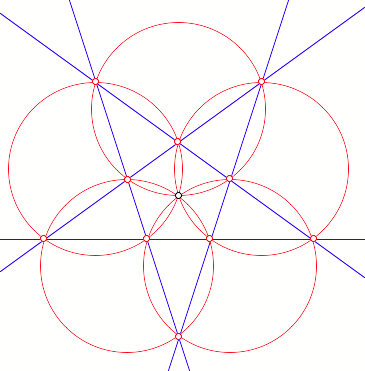
RegelmŠ§iges
Fźnfeck
4.2
RegelmŠ§iges Siebeneck
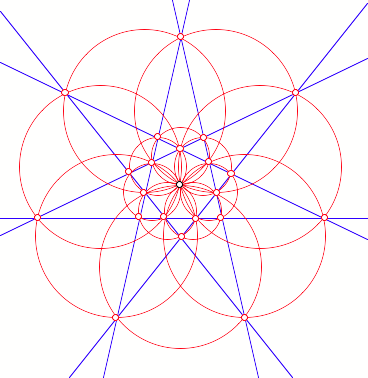
RegelmŠ§iges
Siebeneck
4.3
RegelmŠ§iges Neuneck
RegelmŠ§iges
Neuneck