Hans Walser, [20230121]

Fünf Quadrate

Anregung: Thomas Jahre, Aufgabe 62 - 737

1 Worum geht es?

Puzzle, Zerlegungen, Parkette

2 Problemstellung

Fünf gleich große Quadrate sollen kantenbündig zu einer Figur zusammengesetzt werden, sogenannte Pentominos. Wie viele Pentominos gibt es?

Welche Pentominos lassen sich in vier kongruente Teilfiguren zerlegen?

3 Pentominos

Es gibt zwölf Pentominos (Abb. 0).

Abb. 0: Pentominos

Die Pentominos werden oft mit den großen Buchstaben F, I, L, N, P, T, U, V, W, X, Y, Z gekennzeichnet.

Alle Pentominos haben den Umfang 12, ausgenommen das P, welche aus einem großen und einem kleinen Quadrat besteht. Dieses hat den Umfang 10.

3.1 Ist das Mathematik?

Die didaktische Frage ist, ob die oben formulierte Problemstellung „mathematisch“ ist. Ich fand die Lösung nach der Versuch-und-Irrtum-Methode, also recht unsystematisch. Ich habe auch keinen stringenten Beweis, dass die Aufzählung vollständig ist.

4 Zerlegungen

Die Pentominos sollen in vier zueinander kongruente Teilfiguren zerlegt werden.

4.1 F

Abb. 1: F

4.2 I

Es gibt unendlich viele Lösungen. Im Folgenden einige Beispiele.

Abb. 2: Einige Lösungen

4.3 L

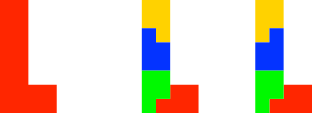
Abb. 3: L

4.4 N

Hier habe ich keine Lösung gefunden.

Abb. 4: N. Keine Zerlegung in vier kongruente Teilfiguren

4.5 P

Die Teilfiguren sind ähnlich zur Gesamtfigur. Die Gesamtfigur hat den minimalen Umfang 10.

Abb. 5: P

4.6 T

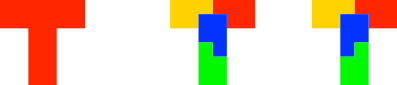
Abb. 6: T

4.7 U

Abb. 7: U

4.8 V

Für das V habe ich keine Lösung gefunden.

Abb. 8: V. Keine Zerlegung in vier kongruente Teilfiguren

4.9 W

Für das W habe ich keine Lösung gefunden.

Abb. 9: W. Keine Zerlegung in vier kongruente Teilfiguren

4.10 X

Unendlich viele Lösungen. Die Abbildung 10 zeigt einige Beispiele.

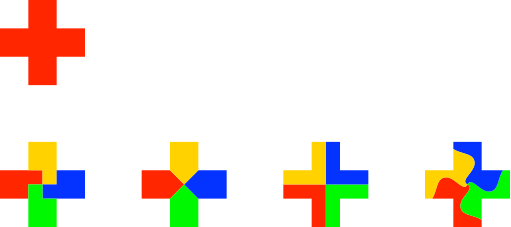
Abb. 10: Es is halt a Kreiz! A Kreiz is'! O mei!

4.11 Y

Abb. 11: Y

4.12 Z

Abb. 12: Z

5 Zusammenfassung

Nicht alle Figuren lassen eine Zerlegung in vier kongruente Teilfiguren zu.

Wenn es aber eine Lösung gibt, ist immer auch die Lösung mit dem Pentomino P (Abb. 5) möglich. Mit Ausnahme des I (Abb. 2) ist das die einzige Figur mit zur Gesamtfigur ähnlichen Teilfiguren. Mit Ausnahme des I (Abb. 2) und des X (Abb. 10) sind ausschließlich Zerlegungen mit den Teilfiguren der Abbildung 6 möglich.

Krummlinig begrenzte Teilfiguren sind nur im Kontext der Punktsymmetrie möglich (Abb. 2 und 10).

Websites

Thomas Jahre, Aufgabe 62 -737

https://www.schulmodell.eu/aufgabe-der-woche.html

Hans Walser: Sierpinski-T

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski-T/Sierpinski-T.html

Hans Walser: Iterationen

http://www.walser-h-m.ch/hans/Miniaturen/I/Iterationen/Iterationen.html

Hans Walser: Iterationen

http://www.walser-h-m.ch/hans/Miniaturen/I/Iterationen2/Iterationen2.html

Wikipedia: Pentomino

https://de.wikipedia.org/wiki/Pentomino

Literatur

Mann, Thomas (1901): Buddenbrooks. Verfall einer Familie. S. Fischer Verlag, Berlin 1901, 2 Bde. 566 S., 539 S.