1 Worum geht es?

Elementargeometrische Fragestellung. Zerlegungsgleichheit. Feststellung des Goldenen Schnittes. Rhombenparkett

2 Problemstellung

Gesucht ist ein Rhombus, in welchen sich zwei gleich große regelmäßige Fünfecke gemäß der Abbildung 1 einpassen lassen.

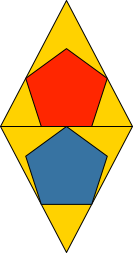
Abb. 1: Zwei gleiche Fünfecke

3 Konstruktion

Die Konstruktion geht so (Abb. 2): Wir zeichnen zwei Fünfecke in der gewünschten Position. Dann klappen wir das untere Fünfeck nach oben. Nun haben wir genug Anhaltspunkte, um das Profil der oberen Rhombenhälfte zu zeichnen. Herunterklappen liefert schließlich den ganzen Rhombus.

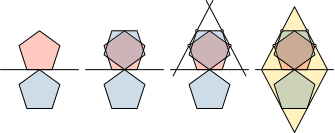
Abb. 2: Konstruktion

4 Zerlegung

Die Teile der beiden Rhombenhälften außerhalb der Fünfecke sind flächen- und damit zerlegungsgleich (Abb. 3).

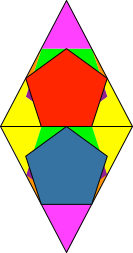
Abb. 3: Zerlegungsgleichheit

5 Der Goldene Schnitt

Der Goldene Schnitt erscheint an verschiedenen Stellen (Abb. 4). Es sind jeweils der Major rot und der Minor blau eingetragen. Nachweis durch Kopfgeometrie.

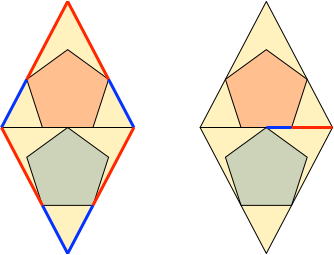
Abb. 4: Der Goldene Schnitt

6 Rhombenparkett

Im Rhombenparkett haben die Fünfecke benachbarter Rhomben gemeinsame Eckpunkte (Abb. 5).

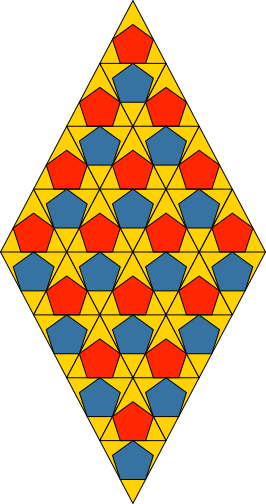
Abb. 5: Rhombenparkett

Die Abbildung 6 zeigt eine Variante.

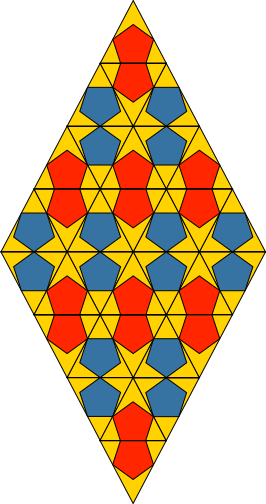
Abb. 6: Variante

Weblinks

Hans Walser: Rechteck im Rhombus

http://www.walser-h-m.ch/hans/Miniaturen/R/Rechteck_im_Rhombus/Rechteck_im_Rhombus.html

Hans Walser: Quadrate im Rhombus

http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadrate_im_Rhombus/Quadrate_im_Rhombus.html