Hans Walser, [20140211]

FŸnfeckapproximation

Anregung und Idee: M. S., J, und M. W.

1     Eine Jugenderinnerung

Als SekundarschŸler (7. und 8. Schuljahr) Ÿberlegte ich mir, dass man zur Konstruktion eines regelmŠ§igen FŸnfecks einen Winkel von 72¡ brŠuchte. Das schaffte ich allerdings nicht, und schlie§lich fragte ich meinen Geometrielehrer, wie man einen Winkel von 72¡ konstruieren kšnne. Seine Antwort: Indem man das regelmŠ§ige FŸnfeck konstruiert. — Voilˆ!

2     Eine Approximation und ihr Hintergrund

Es ist . Das ist etwas mehr als die HŠlfte des gesuchten Winkels von 72¡.

3     Im Karo-Raster

Im Karo-Raster zeichnen wir zunŠchst die Punkte M, A, C, D gemŠ§ Abbildung 1.

Abb. 1: Start im Karo-Raster

Dabei erinnern wir uns an das gute alte Lehrerdreieck mit den Katheten 3 und 4 und der Hypotenuse 5.

Nun halbieren wir den Winkel AMC und erhalten auf dem Umkreis den Punkt B. Die Winkelhalbierende des Winkels AMC kann am einfachsten mit dem in der Abbildung 2 eingezeichneten Rasterpunkt H gezeichnet werden.

Analog finden wir den Punkt E und haben somit approximativ das regelmŠ§ige FŸnfeck ABCDE.

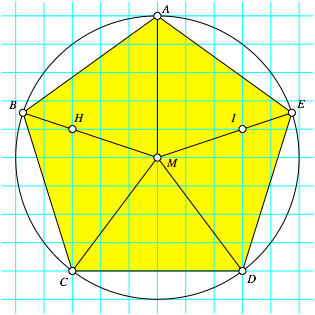
Abb. 2: Approximation des regelmŠ§igen FŸnfeckes

 

4     Scherenschnitt mit fŸnfteiliger Symmetrie

Wir falten ein Origami-Papier gemŠ§ Abbildung 3.

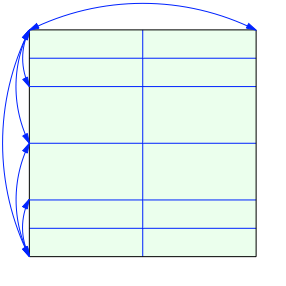
Abb. 3: Start mit Origami-Papier

Die schrŠge Faltlinie der Abbildung 4 fŸhrt zur Approximation des Winkels von 36¡.

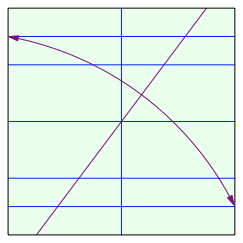
Abb. 4: Die entscheidende Faltlinie

Schlie§lich falten wir das Papier zum Spickel mit dem in der Abbildung 5 markierten roten Dreieck als Deckblatt. Dies geht auf verschiedene Weisen.

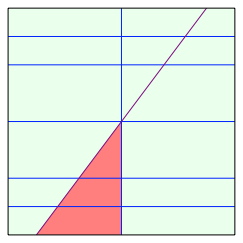
Abb. 5: Der entscheidende Spickel

Dieser Spickel kann nun mit der Schere kreativ bearbeitet werden. Auffalten liefert einen Scherenschnitt mit fŸnfteiliger Symmetrie. Die Abbildung 6 zeigt ein Beispiel.

Abb. 6: Scherenschnitt

In (Walser, 2013, S. 93-101) werden exakte Faltprozesse fŸr FŸnfeck und zugehšrige Scherenschnitte besprochen.

 

Literatur

Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.