Hans Walser, [20141203a]
Funktionenfolge
1 Worum geht es?
Es wird eine Funktionenfolge besprochen, die mit dem Goldenen Schnitt zu tun hat.
2 Die Folge der Funktionen
Zu 
definieren
wir die Funktion
Die
Abbildung 1 zeigt die Funktionsgrafen fŸr 
. FŸr gerade n
sind die Funktionsgrafen rot, fŸr ungerade n
blau gezeichnet.
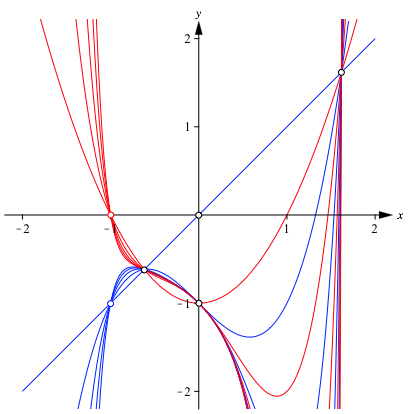
Abb. 1: Funktionsgrafen
3 Gemeinsame Punkte
FŸr
ungerades n haben alle Funktionen
eine Nullstelle bei 
. Dies folgt unmittelbar aus der Definition der Funktionenfolge.
FŸr
gerades n verlaufen alle
Funktionsgrafen durch 
. Auch diese folgt unmittelbar aus der Definition der
Funktionenfolge.
FŸr alle 
verlaufen
die Funktionsgrafen durch 
. Ebenfalls trivial.
Und nun
wird es spannend. Mit der Bezeichnung 
(Goldener
Schnitt) verlaufen alle Funktionsgrafen durch 
und 
. FŸr den Beweis verwenden wir die Relation 
. Es ist dann:
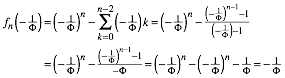
Analog ist:
4 Nullstellen
FŸr
gerade n haben wir die Nullstelle 
sowie eine
zweite, positive Nullstelle im Intervall 
. FŸr ungerade n
haben wir eine einzige Nullstelle, diese liegt im Intervall 
. Die Tabelle 1 zeigt die Nullstellen in AbhŠngigkeit
von n.
|
n |
Nullstelle |
|
|
n |
Nullstelle |
|
|
n |
Nullstelle |
|
1 |
0. |
|
|
17 |
1.617830929 |
|
|
33 |
1.618033897 |
|
2 |
1. |
|
|
18 |
1.617908582 |
|
|
34 |
1.618033932 |
|
3 |
1.324717957 |
|
|
19 |
1.617956520 |
|
|
35 |
1.618033954 |
|
4 |
1.465571232 |
|
|
20 |
1.617986125 |
|
|
36 |
1.618033967 |
|
5 |
1.534157745 |
|
|
21 |
1.618004414 |
|
|
37 |
1.618033975 |
|
6 |
1.570147312 |
|
|
22 |
1.618015713 |
|
|
38 |
1.618033980 |
|
7 |
1.590005374 |
|
|
23 |
1.618022695 |
|
|
39 |
1.618033984 |
|
8 |
1.601347334 |
|
|
24 |
1.618027009 |
|
|
40 |
1.618033986 |
|
9 |
1.607982728 |
|
|
25 |
1.618029675 |
|
|
41 |
1.618033987 |
|
10 |
1.611930397 |
|
|
26 |
1.618031323 |
|
|
42 |
1.618033988 |
|
11 |
1.614306823 |
|
|
27 |
1.618032341 |
|
|
43 |
1.618033988 |
|
12 |
1.615749203 |
|
|
28 |
1.618032970 |
|
|
44 |
1.618033988 |
|
13 |
1.616629684 |
|
|
29 |
1.618033359 |
|
|
45 |
1.618033988 |
|
14 |
1.617169296 |
|
|
30 |
1.618033600 |
|
|
46 |
1.618033989 |
|
15 |
1.617500905 |
|
|
31 |
1.618033748 |
|
|
47 |
1.618033989 |
|
16 |
1.617705070 |
|
|
32 |
1.618033840 |
|
|
48 |
1.618033989 |
Tab. 1: Nichtnegative Nullstelle
Die
Nullstellen streben gegen den Goldenen Schnitt 
. Eigentlich ist das schon aus der Abbildung 1 klar.
Beweisskizze: Wir haben die Gleichung
zu lšsen. FŸr x > 1 kann dies umgeformt werden zu:
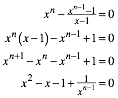
FŸr 
verschwindet der Stšrterm 
und es
bleibt die quadratische Gleichung 
mit der
Lšsung 
Ÿbrig.
5 Rekursive Definition
Die Funktionenfolge kann rekursiv definiert werden:
Damit lassen sich die gemeinsamen Punkte (Abschnitt 3) ebenfalls nachweisen.
6 Ein Kreis
Vier der
in Abschnitt 3 beschriebenen Punkte liegen auf einem Kreis (Abb. 2). Dieser hat
den Mittelpunkt 
und den Radius
.
Abb. 2: Kreis