Hans Walser, [20180514]
Goldener Schnitt im Quadrat
1 Worum geht es?
Konstruktionen des Goldenen Schnittes auf der Basis eines Quadrates und dessen Umkreis.
Es handelt sich um Varianten der Konstruktion von George Odom.
2 Minor-Major-Minor
Wir unterteilen ein Quadrat in einen 3×3-Raster und zeichnen seinen Umkreis (Abb. 1).

Abb. 1: Raster und Umkreis
Durch eine Diagonale eines kleinen Eckquadrates erhalten wir den Goldenen Schnitt in der Reihenfolge Minor-Major-Minor (Abb. 2).
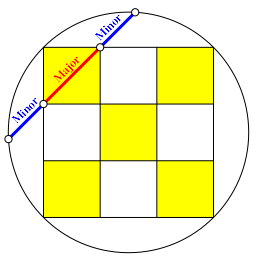
Abb. 2: Minor-Major-Minor
Nachweis durch Rechnen. Ein schšner geometrischer Beweis ist mir nicht gelungen.
Die Situation im Quadratraster ist dieselbe wie bei [1]. Die Abbildung 3 zeigt die †berlagerung der beiden Konstruktionen.

Abb. 3: †berlagerung der beiden Konstruktionen
3 Major-Minor-Major
Fźr die umgekehrte Reihenfolge braucht es mehr Aufwand.
Wir beginnen mit einem 2×2-Raster (Abb. 4).

Abb. 4: Raster
Anschlie§end verlŠngern wir die linke und die obere Seite gemŠ§ Abbildung 5. Dieser Schritt lŠsst den Goldenen Schnitt erahnen.
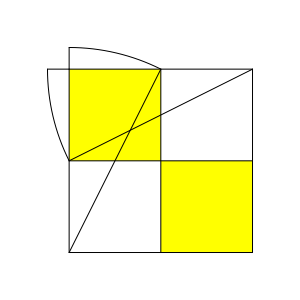
Abb. 5: VerlŠngerung der Seiten
Wir ergŠnzen zu einem leicht grš§eren Quadrat und zeichnen dessen Umkreis (Abb. 6).
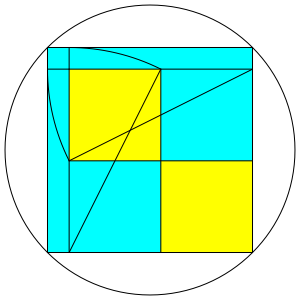
Abb. 6: Quadrat und Umkreis
Nun kšnnen wir mit einer der beiden Diagonalen des kleinen Quadrates links oben arbeiten (Abb. 7) und erhalten den Goldenen Schnitt in der Reihenfolge Major-Minor-Major. Beweis durch Nachrechnen.
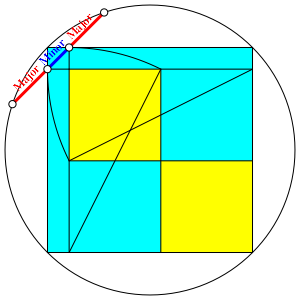
Abb. 7: Major-Minor-Major
Literatur und Websites
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
[1] Walser, Hans: Goldener Schnitt im Kreuz
www.walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_im_Kreuz/Goldener_Schnitt_im_Kreuz.htm